Ask questions which are clear, concise and easy to understand.
Ask QuestionPosted by Tîtûs Tîtûs À 1 month, 2 weeks ago
- 0 answers
Posted by Tîtûs Tîtûs À 1 month, 2 weeks ago
- 0 answers
Posted by Swati Mahadik 6 months, 4 weeks ago
- 0 answers
Posted by Tanisha Mukati 7 months, 3 weeks ago
- 0 answers
Posted by Harsh Tripathi Tripathi 9 months, 1 week ago
- 0 answers
Posted by Abhi Choudhary 11 months, 2 weeks ago
- 0 answers
Posted by Abhi Choudhary 11 months, 2 weeks ago
- 1 answers
Posted by Disha Jain 11 months, 2 weeks ago
- 0 answers
Posted by Gaurav Purohit 11 months, 3 weeks ago
- 0 answers
Posted by Mayank Gaming 1 year ago
- 1 answers
Posted by Ayushi Soni 1 year, 1 month ago
- 1 answers
Posted by Harshwardhan Singh Rajput 1 year, 3 months ago
- 0 answers
Posted by Khilesh Maskare 1 year, 3 months ago
- 0 answers
Posted by Khilesh Maskare 1 year, 3 months ago
- 1 answers
Preeti Dabral 1 year, 3 months ago
The Venn diagram for {tex}(A \cap B)'{/tex}The shaded portion represents {tex}(A \cap B)'{/tex}
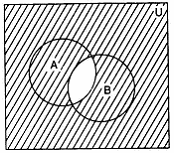
Posted by Soumya Nema 1 year, 3 months ago
- 0 answers
Posted by Ayush Verma 8 months, 2 weeks ago
- 0 answers
Posted by Ankit Meena 1 year, 6 months ago
- 1 answers
Posted by Op Ankit 1 year, 6 months ago
- 1 answers
Preeti Dabral 1 year, 6 months ago
{tex}\begin{aligned} & \text { Let } y=f(x)=\operatorname{cosec} x \\ & \therefore f(x+h)=\operatorname{cosec}(x+h) \\ & \therefore \frac{d y}{d t}=\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} \\ & =\lim _{h \rightarrow 0} \frac{\operatorname{cosec}(x+h)-\operatorname{cosec} x}{h} \\ & =\lim _{h \rightarrow 0} \frac{1}{h}\left[\frac{1}{\sin (x+h)}-\frac{1}{\sin x}\right] \\ & =\lim _{h \rightarrow 0} \frac{\sin x-\sin (x+h)}{h \cdot \sin x \cdot \sin (x+h)} \\ & =\lim _{h \rightarrow 0} \frac{2 \cos \left(\frac{2 x+h}{2}\right) \sin \left(-\frac{h}{2}\right)}{h \cdot \sin x \sin (x+h)} \\ & =-\lim _{h \rightarrow 0} \frac{\cos \left(x+\frac{h}{h}\right)}{\sin x \cdot \sin (u+h)} \cdot \lim _{h \rightarrow 0} \frac{\sin \frac{h}{2}}{h / 2} \\ & =-\frac{1 \cos x}{\sin x \cdot \sin x} \cdot \lim _{z \rightarrow 0} \frac{\sin z}{z} \\ & {\left[z=\frac{h}{2} \text {; Then, } z \rightarrow 0 \text { when } \Rightarrow h \rightarrow 0\right]} \\ & =\frac{-\cos x}{\sin x \cdot \sin x} \cdot 1 \\ & =-\frac{\cos x}{\sin x} \cdot \frac{1}{\sin x} \\ & =-\operatorname{cosec} x . \cot x \\ & \therefore \frac{d y}{d x}=-1 \operatorname{csec} x \cdot \cot x \\ & \end{aligned}{/tex}
Posted by Sonam Tomar 1 year, 6 months ago
- 1 answers
Posted by Nikhil Piplodiya 1 year, 7 months ago
- 1 answers
Posted by Dattaraj Patil 1 year, 7 months ago
- 0 answers
Posted by Nitin Parihar 1 year, 7 months ago
- 1 answers
Preeti Dabral 1 year, 7 months ago
Here total number of digits = 10
Number of digits used (no digit is repeated) = 4
Since 0 cannot be filled in the fourth place, so number of permutations for fourth place = 9
Now the remaining three places can be filled with 9 digits.
{tex}\therefore {/tex} Number of permutations = {tex}^9{P_3}{/tex}
{tex}= \frac{{9!}}{{6!}} = \frac{{9 \times 8 \times 7 \times 6!}}{{6!}} = 504{/tex}
Hence total number of permutations {tex}= 9 \times 504 = 4536{/tex}
Posted by Neha Thakre 1 year, 7 months ago
- 0 answers
Posted by A S Creation. 1 year, 8 months ago
- 0 answers
Posted by Harsh Dhote 1 year, 8 months ago
- 0 answers
Posted by Suryansh Dwivedi 1 year, 8 months ago
- 1 answers
Posted by Nirjala Dhakad 1 year, 8 months ago
- 0 answers

myCBSEguide
Trusted by 1 Crore+ Students

Test Generator
Create papers online. It's FREE.
CUET Mock Tests
75,000+ questions to practice only on myCBSEguide app
 myCBSEguide
myCBSEguide