
myCBSEguide App
Download the app to get CBSE Sample Papers 2023-24, NCERT Solutions (Revised), Most Important Questions, Previous Year Question Bank, Mock Tests, and Detailed Notes.
Install NowCBSE Sample Question Paper for Class 11 Mathematics – in PDF
As we know, CBSE has released the new marking scheme and blueprint for Class 11, you can get new sample papers (2023-24) accordingly from from the myCBSEguide app and our Student Dashboard. We are providing Mathematics sample papers for CBSE class 11 exams. The Sample Papers are available for free download on the myCBSEguide app and website in PDF format. These CBSE Sample Papers for Class 11 Mathematics with Solutions will surely help students get good scores in exams.
Download Mathematics Sample Papers as PDF
CBSE Sample Papers Class 11 Mathematics 2023-24
myCBSEguide provides CBSE Class 11 Sample Papers of Mathematics for the current session 2023-24 with solutions in PDF format for free download. We advise students to download new pattern model question papers and practice them regularly. Class 11 Mathematics New Sample Papers follow the blueprint of the current session only. Students must check the latest syllabus and marking scheme. Sample papers for Class 11 Mathematics and other subjects are available for download as PDFs in our app too. myCBSEguide provides sample papers with solutions for the session 2023-24 as per the new exam pattern.

Marking Scheme for the Class 11 exam 2024
If you go through the latest model paper, you will find that CBSE has updated the marking scheme of the exam this year. Now, CBSE is asking only 2, 3 and 5 marks subjective questions. The weightage of objective-type questions is fair enough this year. So, no student can ignore them in any case. That’s why we recommend you not to follow the selective-study method. Try to cover the whole syllabus on time and revise as much as possible.
Apart from these subjective questions, CBSE will also ask MCQs, ARQs (assertion & reason) and CBQs (Case Study) type questions in the 2023-2024 annual exams.
Class 11 – Mathematics Sample Paper (2023-24)
Maximum Marks: 80
Time Allowed: : 3 hours
General Instructions:
- This Question paper contains – five sections A, B, C, D and E. Each section is compulsory. However, there are internal choices in some questions.
- Section A has 18 MCQ’s and 02 Assertion-Reason based questions of 1 mark each.
- Section B has 5 Very Short Answer (VSA)-type questions of 2 marks each.
- Section C has 6 Short Answer (SA)-type questions of 3 marks each.
- Section D has 4 Long Answer (LA)-type questions of 5 marks each.
- Section E has 3 source based/case based/passage based/integrated units of assessment (4 marks each) with sub parts.
Class 11 Maths Sample Paper Section A
- If cos x = {tex}\frac{1}{2}{/tex}, then cos 3x = ?a) -1b) {tex}\frac{2}{3}{/tex}c) {tex}\frac{3}{2}{/tex}d) {tex}\frac{1}{6}{/tex}
- If R is a relation on the set A = {1, 2, 3, 4, 5, 6, 7, 8, 9} given by x R y {tex}\Leftrightarrow{/tex} y = 3x, then R =a) {(3, 1), (2, 6), (3, 9)}b) {(3, 1), (6, 2), (9, 3)}c) {(3, 1), (6, 2), (8, 2), (9, 3)}d) none of these
- A dice is tossed once and even number has come up. The chance that it is either 2 or 4 isa) none of theseb) {tex}\frac{2}{3}{/tex}c) {tex}\frac{1}{3}{/tex}d) {tex}\frac{5}{6}{/tex}
- {tex}\lim\limits_{x \to 0} \frac{(1+x)^n-1}{x}{/tex} is equal toa) -nb) 1c) 0d) n
- The inclination of the straight line passing through the point (-3, 6) and the mid-point of the line joining the point (4, -5) and (-2 ,9) isa) {tex}\frac {3\pi} {4}{/tex}b) {tex}\frac {\pi} {3}{/tex}c) {tex}\frac {\pi} {4}{/tex}d) {tex}\frac {\pi} {6}{/tex}
- If A {tex}\subset{/tex} B, thena) {tex}{ A }^{ c }\subset { B }^{ c }{/tex}b) {tex}{ B }^{ c }⊄{ A }^{ c }{/tex}c) {tex}{ A }^{ c }={ B }^{ c }{/tex}d) {tex}{ B }^{ c }\subset { A }^{ c }{/tex}
To practice more questions & prepare well for exams, download myCBSEguide App. It provides complete study material for CBSE, NCERT, JEE (main), NEET-UG and NDA exams. Teachers can use Examin8 App to create similar papers with their own name and logo.
- Mark the correct answer for (1 + i)-1 =?a) {tex}\left(\frac{-1}{2}+\frac{1}{2} i\right){/tex}b) None of thesec) {tex}\left(\frac{1}{2}-\frac{1}{2} i\right){/tex}d) (2 – i)
- The range of the function f(x) = {tex}\frac{x^2-x+1}{x^2+x+1}{/tex} isa) none of theseb) [3, {tex}\infty {/tex})c) Rd) {tex}\left[\frac{1}{3}, 3\right]{/tex}
- What is the solution set for {tex}\frac{|x-2|}{x-2}>0{/tex}?a) (2, {tex}\infty {/tex})b) none of thesec) (-{tex}\infty {/tex}, -2)d) (0, 2)
- A horse is tied to a post by a rope. If the horse moves along a circular path, always keeping the rope tight and describes 88 m when it traces 72° at the centre, then the length of the rope isa) 22 mb) 70 mc) 35 md) 17.5 m
- If A = {1, 2, 3}, and B = {1, 3, 5, 7}, then A {tex}\cup{/tex} B =a) none of theseb) {1, 3, 5, 7}c) {1, 2, 3, 7}d) {1, 2, 3, 5, 7}
- The 17th term of the GP 2, {tex}\sqrt{8}{/tex}, 4, {tex}\sqrt{32 }{/tex}… isa) 256b) {tex}256 \sqrt{2}{/tex}c) {tex}128 \sqrt{2}{/tex}d) 512
- {tex}\left\{\frac{c_{1}}{c_{0}}+2 \frac{C_{2}}{C_{1}}+\right.{/tex}{tex}\left.3 \frac{C_{3}}{C_{2}}+\ldots+n \cdot \frac{C_{n}}{C_{n-1}}\right\}{/tex} = ?a) {tex}\frac{1}{2} n(n+1){/tex}b) 2nc) 2n-1d) 2n
- If a, b, c are real numbers such that a {tex}\leq{/tex} b, c < 0, thena) ac {tex}\leq{/tex} bcb) ac > bcc) ac {tex} \geq{/tex} bcd) none of these
- If A and B are two given sets , then A {tex}\cap{/tex} (A {tex}\cap{/tex} B)c is equal toa) Bb) Ac) A {tex}\cap{/tex} Bcd) {tex}\phi {/tex}
- The value of sin 20° sin 40° sin 60° sin 80° isa) {tex}\frac{-3}{16}{/tex}b) {tex}\frac{3}{16}{/tex}c) {tex}\frac{1}{16}{/tex}d) {tex}\frac{5}{16}{/tex}
- If z = 1 – cos {tex}\theta{/tex} + i sin {tex}\theta{/tex}, then |z| =a) {tex}2\left|\sin \frac{\theta}{2}\right|{/tex}b) {tex}2\left|\cos \frac{\theta}{2}\right|{/tex}c) 2 cos {tex}\frac{\theta}{2}{/tex}d) 2 sin {tex}\frac{\theta}{2}{/tex}
- If in a group of n distinct objects, the number of arrangements of 4 objects is 12 times the number of arrangements of 2 objects, then the number of objects isa) 8b) 6c) None of thesed) 10
- Assertion (A): Number of terms in the expansion of {tex}\left(2 x-\frac{4}{x^2}\right)^{10}{/tex} is 11.
Reason (R): Number of terms in the expansion of, (x + a)n is n + 1.a) Both A and R are true and R is the correct explanation of A.b) Both A and R are true but R is not the correct explanation of A.c) A is true but R is false.d) A is false but R is true. - Consider the following data
xi 4 8 11 17 20 24 32 fi 3 5 9 5 4 3 1 Assertion (A): The variance of the data is 45.8.
Reason (R): The standard deviation of the data is 6.77.a) Both A and R are true and R is the correct explanation of A.b) Both A and R are true but R is not the correct explanation of A.c) A is true but R is false.d) A is false but R is true. Class 11 Maths Sample Paper Section B
- Let A = {1, 2}, B = {2, 3, 4}, C = {4, 5}. Find A {tex}\times{/tex} (B {tex}\cup{/tex} C)
OR
Let A and B be two sets. Show that the sets A {tex}\times{/tex} B and B {tex}\times{/tex} A have an element in common if the sets A and B have an element in common.
- If f(t) {tex}= \frac { 2 } { 9 } t ^ { 4 } – \frac { 5 } { 3 } t ^ { 3 } + 2 t – 1,{/tex}then find f'(-3).
- Find the centre and radius of the circle: (x + 5)2 + (y – 3)2 = 20
OR
On the line joining (1, 0) and (3, 0) an equilateral triangle is drawn, having its vertex in the first quadrant. Find the equation to the circles described on its sides as diameter.
- Is the pair of set A = {2, 3} and B = {x : x is solution of x2 + 5x + 6 = 0} equal? Give reason.
- If A(2, -5), B(-2, 5), C(x, 3) and D(1, 1) be four points such that AB and CD are perpendicular to each other, find the value of x.
Class 11 Maths Sample Paper Section C
- Draw the graph of the function f(x) = {tex}\begin{cases}1+2 x & x<0 \\ 3+5 x, & x \geq 0\end{cases}{/tex}. Also, find its range.
- To receive Grade A, in a course, one must obtain an average of 90 marks or more in five examinations (each of 100 marks). If Sunita’s marks in first four examinations are 87, 92, 94 and 95, find minimum marks that Sunita must obtain in fifth examination to get Grade A in the course.
- Three vertices of a parallelogram ABCD are A(3, -1, 2), B(1, 2, -4) and C(-1, 1, 2). Find the coordinates of the fourth vertex.
OR
Show that the points P(2, 3, 5), Q(-4, 7, -7), R (-2, 1, -10) and S(4, -3, 2) are the vertices of a rectangle.
- Using binomial theorem, expand: {tex}(\sqrt[3]{x}-\sqrt[3]{y})^{6}{/tex}
OR
Show that the coefficient of the middle term in the expansion of(1 + x)2n is equal to the sum of the coefficients of middle terms in the expansion of (1 + x)2n-1.
- Find the square root of -8 – 6i
OR
Find the real values of x and y for which: (x + iy)(3 – 2i) = (12 + 5i)
- Let A, B and C be the sets such that {tex}A \cup B = A \cup C{/tex} and {tex}A \cap B = A \cap C{/tex}. Show that B = C.
Class 11 Maths Sample Paper Section D
- One urn contains two black balls (labelled B1 and B2) and one white ball. A second urn contains one black ball and two white balls (labelled W1 and W2). Suppose the following experiment is performed. One of the two urns is chosen at random. Next a ball is randomly chosen from the urn. Then a second ball is chosen at random from the same urn without replacing the first ball.
- Write the sample space showing all possible outcomes
- What is the probability that two black balls are chosen?
- What is the probability that two balls of opposite colour are chosen?
- Evaluate: {tex}\lim_{x\rightarrow0}\frac{1-\cos x\cos2x\cos3x}{\sin^22x}{/tex}
OR
- If {tex}f(x) = \left\{ {\begin{array}{*{20}{c}} {|x| + 1,}&{x < 0} \\ {0,}&{x = 0} \\ {|x| – 1,}&{x > 0} \end{array}} \right.,{/tex} for what values (s) of a does {tex}\mathop {\lim }\limits_{x \to a} f(x){/tex} exist?
- Find the derivative of the function {tex}\cos \left( x – \frac { \pi } { 8 } \right){/tex} from the first principle.
- The lengths of three unequal edges of a rectangular solid block are in GP. The volume of the block is 216 cm3 and the total surface area is 252 cm2. Find the length of the longest edge.
- At the foot of a mountain the elevation of its summit is 45o; after ascending 1000 m towards the mountain up a slope of 30o inclination, the elevation is found to be 60o. Find the height of the mountain.
OR
Prove: {tex}\left(\frac{1}{\sec ^{2} x-\cos ^{2} x}+\frac{1}{\csc ^{2} x-\sin ^{2} x}\right){/tex} sin2x cos2x = {tex}\frac{1-\sin ^{2} x \cos ^{2} x}{2+\sin ^{2} x \cos ^{2} x}{/tex}
Class 11 Maths Sample Paper Section E
- Read the text carefully and answer the questions:
A satellite dish has a shape called a paraboloid, where each cross section is parabola. Since radio signals (parallel to axis) will bounce off the surface of the dish to the focus, the receiver should be placed at the focus. The dish is 12 ft across, and 4.5 ft deep at the vertex.
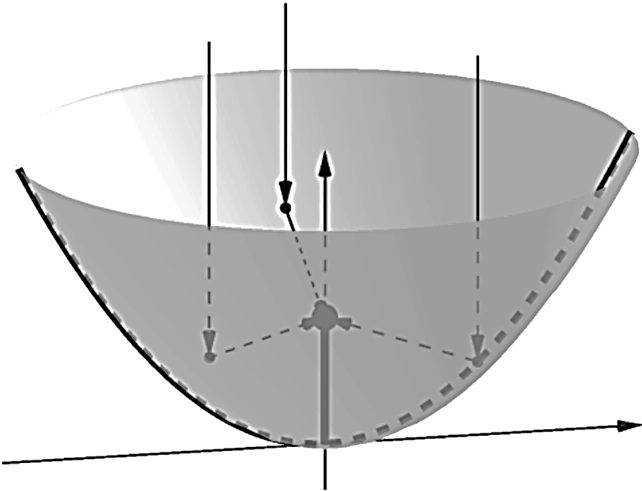
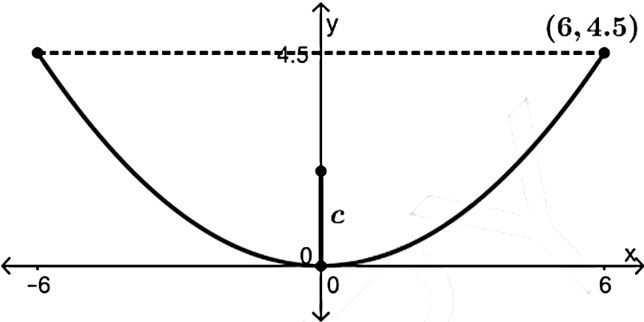
- Name the type of curve given in the above paragraph and find the equation of curve?
- Find the equation of parabola whose vertex is (3, 4) and focus is (5, 4).
- Find the equation of parabola Vertex (0, 0) passing through (2, 3) and axis is along x-axis. and also find the length of latus rectum.
OR
Find focus, length of latus rectum and equation of directrix of the parabola x2 = 8y.
To practice more questions & prepare well for exams, download myCBSEguide App. It provides complete study material for CBSE, NCERT, JEE (main), NEET-UG and NDA exams. Teachers can use Examin8 App to create similar papers with their own name and logo.
- Read the text carefully and answer the questions:
Consider the dataxi 4 8 11 17 20 24 32 fi 3 5 9 5 4 3 1 - Find the standard deviation.
- Find the variance.
- Find the mean.
OR
Write the formula of variance?
- Read the text carefully and answer the questions:
Ashish is writing examination. He is reading question paper during reading time. He reads instructions carefully. While reading instructions, he observed that the question paper consists of 15 questions divided in to two parts – part I containing 8 questions and part II containing 7 questions.

- If Ashish is required to attempt 8 questions in all selecting at least 3 from each part, then in how many ways can he select these questions
- If Ashish is required to attempt 8 questions in all selecting 3 from I part, then in how many ways can he select these questions
Class 11 – Maths Sample Paper Solution (2023-24)
Maths need practice. You can’t just read and learn. You have to practice regularly to master Maths. So, there is no shortcut. Just start revising the concepts and practice questions as many as possible. Here, myCBSEguide app will be your perfect study companion. We have thousands of questions that will definitely sharpen your skills every day.
This sample paper is only one example to show. Just download the myCBSEguide app to access many such papers and other important questions. You will get question papers with perfectly explained solutions on the app.
Class 11 Maths Sample Paper Solution Section A
- (a) -1
Explanation: cos 3x = (4 cos3x – 3 cos x) {tex}=\left(4 \times \frac{1}{8}-3 \times \frac{1}{2}\right){/tex}{tex}=\left(\frac{1}{2}-\frac{3}{2}\right){/tex} = -1 - (d) none of these
Explanation: {tex}\therefore{/tex} For A = {1, 2, 3, 4, 5, 6, 7, 8, 9} the satisfying complete relation is:
R = {(1, 3), (2, 6), (3, 9)} - (b) {tex}\frac{2}{3}{/tex}
Explanation: Total number of ways of getting even number is 3
Out of these 3 even numbers we have to get either 2 or 4 which can be done in 2 ways.
So the required probability is {tex}\frac{2}{3}{/tex} - (d) n
Explanation: {tex}\lim \limits_{x \to 0} \frac{(1+x)^n-1^n}{(1+x)-(1)}=\mathop {lim}\limits_{x \to 0}n(1+x)^{n-1}=n{/tex} - (a) {tex}\frac {3\pi} {4}{/tex}
Explanation: The midpoint of the line joining the points (4, -5) and (-2, 9) is (1, 2)
Let {tex}\theta{/tex} be the inclination of the straight line passing through the points (-3, 6) and (1,2).
Then , using slope formula of tan {tex}\theta{/tex} we get ,
tan {tex}\theta=\frac{2-6}{1+3}{/tex} = -1
{tex}\Rightarrow \theta=\frac{3 \pi}{4}{/tex}
To practice more questions & prepare well for exams, download myCBSEguide App. It provides complete study material for CBSE, NCERT, JEE (main), NEET-UG and NDA exams. Teachers can use Examin8 App to create similar papers with their own name and logo. - (d) {tex}{ B }^{ c }\subset { A }^{ c }{/tex}
Explanation: Let A {tex}\subset{/tex} B
To prove Bc {tex}\subset{/tex} Ac, it is enough to show that x {tex}\in{/tex} Bc {tex}\Rightarrow{/tex} x {tex}\in{/tex} Ac
Let x {tex}\in{/tex} Bc
{tex}\Rightarrow{/tex} x {tex}\notin{/tex} B
{tex}\Rightarrow{/tex} x {tex}\notin{/tex} A since A {tex}\subset{/tex} B
{tex}\Rightarrow{/tex} x {tex}\in{/tex} Ac
Hence Bc {tex}\subset{/tex} Ac - (c) {tex}\left(\frac{1}{2}-\frac{1}{2} i\right){/tex}
Explanation: (1 + i)-1 = {tex}\frac{1}{(1+i)}{/tex}= {tex}\frac{1}{(1+i)} \times \frac{(1-i)}{(1-i)}{/tex} = {tex}\frac{(1-i)}{\left(1^{2}-i^{2}\right)}{/tex} = {tex}\frac{(1-i)}{2}{/tex} = {tex}\left(\frac{1}{2}-\frac{1}{2} i\right){/tex} - (d) {tex}\left[\frac{1}{3}, 3\right]{/tex}
Explanation: Let y = {tex} \;\frac{{{{\text{x}}^2} – {\text{x}} + 1}}{{{{\text{x}}^2} + {\text{x}} + 1}}{/tex}
{tex}\Rightarrow{/tex} y (x2 + x + 1) = x2 – x + 1
{tex}\Rightarrow {/tex} (y – 1)x2 + (y + 1)x + y – 1 = 0
For x to be real, we must have
(y + 1)2 – 4(y – 1)2 {tex}\ge{/tex} 0 (Discriminant = b2 – 4ac)
{tex}\Rightarrow{/tex} -3y2 + 10y – 3 {tex}\ge{/tex} 0 {tex}\Rightarrow{/tex} 3y2 – 10y + 3 {tex}\le{/tex} 0
{tex}\Rightarrow{/tex} (3y – 1)(y – 3) {tex}\le{/tex} 0
{tex}\Rightarrow{/tex} {tex}\frac{1}{3} \leq y \leq 3{/tex} {tex}\Rightarrow{/tex} y {tex}\in{/tex} {tex}\left[\frac{1}{3}, 3\right]{/tex}
{tex}\therefore{/tex} Range {tex}{ = \left[ {\frac{1}{3},\;3} \right]}{/tex} - (a) (2, {tex}\infty {/tex})
Explanation: We have |x – 2| {tex}\ge{/tex} 0 [ {tex}\because {/tex} |x| or absolute value of x is always positive or zero but never negative] Now {tex}\frac{|x-2|}{x-2}>0{/tex} {tex}\Rightarrow {/tex} x – 2 > 0 [{tex}\because{/tex} {tex}\frac{a}{b}{/tex} > 0, a {tex}\ge{/tex} 0 {tex}\Rightarrow{/tex} b > 0] {tex}\Rightarrow {/tex} x > 2
{tex}\Rightarrow x\epsilon \left( 2,\infty \right) {/tex} - (b) 70 m
Explanation: {tex}\theta=42^{\circ}=\left(42 \times \frac{\pi}{180}\right)^{c}{/tex}{tex}=\left(\frac{2 \pi}{5}\right)^{c}{/tex} and l = 88 m.
{tex}\therefore r=\frac{l}{\theta}=\left(88 \times \frac{5}{2 \pi}\right) \mathrm{m}{/tex}{tex}=\left(88 \times \frac{5}{2} \times \frac{7}{22}\right) \mathrm{m}{/tex} = 70 m. - (d) {1, 2, 3, 5, 7}
Explanation: Given A = {1, 2, 3} and B = {1, 3, 5, 7}
(A {tex}\cup{/tex} B) = {1, 2, 3, 5, 7} - (d) 512
Explanation: Given GP is 2, 2{tex}\sqrt2{/tex}, 4, 4{tex}\sqrt2{/tex}, …
Here, a = 2 and {tex}=\frac{2 \sqrt{2}}{2}=\sqrt{2}{/tex}
{tex}\therefore T_{17}=a r^{16}=2 \times(\sqrt{2})^{16}=2 \times 2^{8}=2^{9}{/tex} = 512
Therefore, the required 17th term is 512. - (a) {tex}\frac{1}{2} n(n+1){/tex}
Explanation: We know that {tex}\frac{C_{r}}{C_{r 1}}=\frac{n-r+1}{r}{/tex},
Substituting r = 1,2,3,…,n, we obtain
{tex}\frac{C_{1}}{C_{0}}+2 \cdot \frac{C_{2}}{C_{1}}+3 \cdot \frac{C_{3}}{C_{2}}{/tex} + … + {tex}n \cdot \frac{C_{n}}{C_{n-1}}{/tex} = n + (n -1) + (n – 2) + … + 1= {tex}\frac{1}{2} n(n+1){/tex}. - (c) ac {tex} \geq{/tex} bc
Explanation: The sign of the inequality is to be reversed ({tex}\le{/tex} to {tex}\ge{/tex} or {tex}\ge{/tex} to {tex}\le{/tex}) if both sides of an inequality are multiplied by the same negative real number. - (c) A {tex}\cap{/tex} Bc
Explanation: A {tex}\cap{/tex} Bc
A and B are two sets.
A {tex}\cap{/tex} B is the common region in both the sets.
(A {tex}\cap{/tex} Bc) is all the region in the universal set except A {tex}\cap{/tex} B
Now, A {tex}\cap{/tex} (A {tex}\cap{/tex} B)c = A {tex}\cap{/tex} Bc - (b) {tex}\frac{3}{16}{/tex}
Explanation: sin 20° sin 40° sin 60° sin 80°.
= {tex}\frac{\sqrt{3}}{2}{/tex} sin 20° sin (60° – 20°) sin (60° + 20°) (since sin 60° = {tex}\frac{\sqrt{3}}{2}{/tex})
= {tex}\frac{\sqrt{3}}{2}{/tex} sin 20° [sin2 60° – sin2 20°] { sin A + sin B = 2sin{tex}\frac{A+B}2{/tex} cos {tex}\frac{A-B}2{/tex} and sin A – Sin B = 2sin{tex}\frac{A+B}2{/tex} cos{tex}\frac{A-B}2{/tex}
= sin2 60° – sin2 20° = (sin 60° + sin 20°)(sin 60° – sin 20°)
= (2sin40°cos20°)(2sin20°cos40°)
= (2sin40°cos40°) (2sin20°cos 20°) = sin80° sin 40°}
= {tex}\frac{\sqrt{3}}{2}{/tex} sin 20° [ {tex}\frac{3}{4}{/tex} – sin2 20°] = {tex}\frac{\sqrt{3}}{2} \times \frac{1}{4}{/tex} [3sin 20° – 4 sin3 20°] = {tex}\frac{\sqrt{3}}{2} \times \frac{1}{4}{/tex} (sin 60o) (since sin 3{tex}\theta{/tex} = 3sin {tex}\theta{/tex} – 4 sin3{tex}\theta{/tex})
= {tex}\frac{\sqrt{3}}{2} \times \frac{1}{4} \times \frac{\sqrt{3}}{2}=\frac{3}{16}{/tex} - (a) {tex}2\left|\sin \frac{\theta}{2}\right|{/tex}
Explanation: {tex}2\left|\sin \frac{\theta}{2}\right|{/tex}
{tex}\because z=1-\cos \theta+i \sin \theta{/tex}
{tex}\Rightarrow|z|=\sqrt{(1-\cos \theta)^{2}+\sin ^{2} \theta}{/tex}
{tex}\Rightarrow|z|=\sqrt{1+\cos ^{2} \theta-2 \cos \theta+\sin ^{2} \theta}{/tex}
{tex}\Rightarrow|z|=\sqrt{1+1-2 \cos \theta}{/tex}
{tex}\Rightarrow|z|=\sqrt{2(1-\cos \theta)}{/tex}
{tex}\Rightarrow|z|=\sqrt{4 \sin ^{2} \frac{\theta}{2}}{/tex}
{tex}\Rightarrow|z|=2\left|\sin \frac{\theta}{2}\right|{/tex} - (b) 6
Explanation: According to the question:
nP4 = 12 {tex}\times{/tex} nP2
{tex}\Rightarrow \frac{n !}{(n-4) !}{/tex} = 12 {tex}\times \frac{n !}{(n-2) !}{/tex}
{tex}\Rightarrow \frac{(n-2) !}{(n-4) !}{/tex} = 12
{tex}\Rightarrow{/tex} (n – 2) (n – 3) = 4 {tex}\times{/tex} 3
{tex}\Rightarrow{/tex} n – 2 = 4
{tex}\Rightarrow{/tex} n = 6 - (a) Both A and R are true and R is the correct explanation of A.
Explanation: Assertion:
no. of terms = 10 + 1
= 11, True
Reason:
no. of term = n + 1, True
A Reason is correct explanation of Assertion. - (b) Both A and R are true but R is not the correct explanation of A.
Explanation: Assertion: Presenting the data in tabular form, we getxi fi fixi xi – {tex}\bar x{/tex} (xi – {tex}\bar x{/tex})2 fi(xi – {tex}\bar x{/tex})2 4 3 12 -10 100 300 8 5 40 -6 36 180 11 9 99 -3 9 81 17 5 85 3 9 45 20 4 80 6 36 144 24 3 72 10 100 300 32 1 32 18 324 324 30 420 1374 N = 30, {tex}\sum \limits_{i=1}^7 f_i x_i{/tex} = 420, {tex}\sum \limits_{i=1}^7 f_i\left(x_i-\bar{x}\right)^2{/tex} = 1374
Therefore, {tex}\bar{x}=\frac{\sum \limits_{i=1}^7 f_i x_i}{N}=\frac{1}{30} \times 420{/tex} = 14
{tex}\therefore{/tex} Variance {tex}\left(\sigma^2\right)=\frac{1}{N} \sum \limits_{i=1}^7 f_i\left(x_i-\bar{x}\right)^2{/tex}
{tex}\frac {1}{30} \times 1374{/tex} = 458
Reason: Standard deviation {tex}(\sigma)=\sqrt{45.8}{/tex} = 6.77 Class 11 Maths Sample Paper Solution Section B
- Given, A = {1, 2}, B = {2, 3, 4} and C = {4, 5}
B {tex}\cup{/tex} C = {2, 3, 4} {tex}\cup{/tex} {4, 5}
= {2, 3, 4, 5}
{tex}\therefore{/tex} A {tex}\times{/tex} (B {tex}\cup{/tex} C) = {1, 2} {tex}\times{/tex} {2, 3, 4, 5}
= {(1, 2), (1, 3), (1, 4), (1, 5), (2, 2), (2, 3), (2, 4), (2, 5)}OR
Let (a, b) be an arbitrary element of (A {tex}\times{/tex} B) {tex}\cap{/tex} (B {tex}\times{/tex} A). Then,
(a, b) {tex}\in{/tex} (A {tex}\times{/tex} B) {tex}\cap{/tex} (B {tex}\times{/tex} A)
= (a, b) {tex}\in{/tex} A {tex}\times{/tex} B and (a, b) {tex}\in{/tex} B {tex}\times{/tex} A
= (a {tex}\in{/tex} A and b {tex}\in{/tex} B) and (a {tex}\in{/tex}B and b {tex}\in{/tex} A)
= (a {tex}\in{/tex} A and a {tex}\in{/tex} B) and ( b {tex}\in{/tex} A and b {tex}\in{/tex} B)
= a {tex}\in{/tex} A {tex}\cap{/tex} B and b {tex}\in{/tex} A {tex}\cap{/tex} B
Hence, the sets A {tex}\times{/tex} B and B {tex}\times{/tex} A have an element in common if the sets A and B have an element in common. - We have, {tex}f ( t ) = \frac { 2 } { 9 } t ^ { 4 } – \frac { 5 } { 3 } t ^ { 3 } + 2 t – 1{/tex}
On differentiating both sides w.r.t. t, we get
{tex}f ^ { \prime } ( t ) = \frac { 2 } { 9 } \left( 4 t ^ { 3 } \right) – \frac { 5 } { 3 } \left( 3 t ^ { 2 } \right) + 2 ( 1 ) – 0{/tex}{tex}\left[ \because \frac { d } { d t } \left( t ^ { n } \right) = n t ^ { n – 1 } \right]{/tex}
{tex}= \frac { 8 } { 9 } t ^ { 3 } – 5 t ^ { 2 } + 2{/tex}
{tex}\therefore f ^ { \prime } ( – 3 ) = \frac { 8 } { 9 } ( – 3 ) ^ { 3 } – 5 ( – 3 ) ^ { 2 } + 2{/tex}[put t = -3] {tex}= 8 \times \frac { ( – 27 ) } { 9 } – 5 ( 9 ) + 2{/tex}= 8(-3) – 45 + 2
= -24 – 45 + 2 = -67 - Given, (x + 5)2 + (y – 3)2 = 20
The general form of the equation of a circle is:
(x – h)2 + (y – k)2 = r2
Where, (h, k) is the centre of the circle.
r is the radius of the circle.
Comparing the given equation of circle with general form we get:
h = – 5 , k = 3, r2 = 20
{tex}\Rightarrow{/tex} Centre = (-5, 3) and radius = {tex}\sqrt{20}=2 \sqrt{5}{/tex} units.OR
Let (1, 0) and (3, 0) be the coordinate of the points A and B respectively Then
{tex}A B=\sqrt{(1-3)^{2}+(0-0)^{2}}=2{/tex}
let Coordinates of C is C(x1,y1)
Now, {tex}A C=\sqrt{\left(x_{1}-1\right)^{2}+\left(y_{1}-0\right)^{2}}, \quad B C=\sqrt{\left(x_{1}-3\right)^{2}+\left(y_{1}-0\right)^{2}}{/tex}
AC = BC
{tex}A C^{2}=B C^{2}{/tex}
{tex}\left(x_{1}-1\right)^{2}+y_{1}^{2}=\left(x_{1}-3\right)^{2}+y_{1}^{2} \Rightarrow 4 x_{1}=8 \Rightarrow x_{1}=2{/tex}
Again AC = 2
{tex}\sqrt{\left(x_{1}-1\right)^{2}+y_{1}^{2}}=2{/tex}
{tex}\left(x_{1}-1\right)^{2}+y_{1}^{2}=4{/tex}
{tex}(2-1)^{2}+y_{1}^{2}=4 \Rightarrow y_{1}=\pm \sqrt{3} \Rightarrow y_{1}=\sqrt{3}{/tex}
So, the coordinated of are {tex}(2, \sqrt{3}){/tex}
Similarly, the equations of circles with AB and BC as diameters are
(x -1) (x – 3) + (y – 0) (y – 0) = 0 and, (x – 3) (x – 2) + (y – 0) {tex}(y-\sqrt{3})=0{/tex}
or x2 + y2 – 4x + 3 = 0 and, x2 + y2 – 5x – {tex}\sqrt{3} y+6=0{/tex} respectively, - A = {2, 3} and B = {x : x is solution of x2 + 5x + 6 = 0}
Now x2 + 5x + 6 = 0 {tex}\Rightarrow{/tex} x2 + 3x + 2x + 6 = 0
{tex}\Rightarrow{/tex} (x + 3)(x + 2) = 0 {tex}\Rightarrow{/tex} x = -3, -2
{tex}\therefore{/tex} B = {-2, -3}
Hence A and B are not equal sets. - For two lines to be perpendicular, their product of slope must be equal to -1.
Given points are A(2, -5), B(-2, 5) and C(x, 3), D(1, 1)
Therefore, slope ={tex}\left(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\right){/tex}
{tex}\Rightarrow{/tex}Slope of line AB is equal to
{tex}\left(\frac{5+5}{-2-2}\right){/tex}
{tex}=\left(\frac{10}{-4}\right){/tex}
{tex}=\left(\frac{-5}{2}\right){/tex} = -2.5
And the slope of line CD is equal to
{tex}\left(\frac{1-3}{1-x}\right){/tex}{tex}=\left(\frac{-2}{1-x}\right){/tex}
Their product must be equal to -1
the slope of line AB {tex}\times{/tex} Slope of line CD = -1
{tex}\Rightarrow-2.5 \times\left(\frac{-2}{1-x}\right){/tex} = -1
{tex}\Rightarrow{/tex} 5 = x -1
{tex}\Rightarrow{/tex} x = 6 is the required value. Class 11 Maths Sample Paper Solution Section C
- Given, f(x) = {tex}\begin{cases}1+2 x & x<0 \\ 3+5 x, & x \geq 0\end{cases}{/tex}
Here, f(x) = 1 + 2x, x < 0, this gives
f(-4) =1 + 2(-4) = -7
f(-3) = 1 + 2(-3) = -5
f(-2) = 1 + 2(-2) = -3
f(-1) = 1 + 2(-1) = -1
f(x) = 3 + 5x, x {tex}\geq{/tex}0
f(0) = 3 + 5(0) = 3
f(1) = 3 + 5(1) = 8
f(2) = 3 + 5(2) = 13
f(3) = 3 + 5(3) = 18
f(4) = 3 + 5(4) = 23
Now the graph of f is as shown in following figure
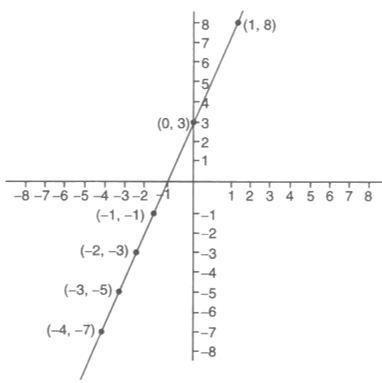
Range: Let y1 = f(x), x < 0
{tex}\therefore {/tex} y1 = 1 + 2x, x < 0
{tex}\therefore{/tex} {tex}x=\frac{y_1-1}{2}, x< 0 {/tex}
{tex}\because x<0 \Rightarrow y_1-1<0 \Rightarrow y_1<1{/tex}
Let y2 = f(x), x {tex}\geq{/tex} 0
{tex}\Rightarrow{/tex} y2 = 3 + 5x, x {tex}\geq{/tex} 0
{tex}\Rightarrow x=\frac{y_2-3}{5}, x \geq 0{/tex}
{tex}\because x \geq 0 \Rightarrow y_2-3 \geq 0 \Rightarrow y_2 \geq 3{/tex}
Therefore, range of f{tex}(-\infty, 1), \cup[3, \infty){/tex} - Let the marks obtained by Sunita in fifth examination be x.
Then average of five examinations {tex} = \frac{{87 + 92 + 94 + 95 + x}}{5}{/tex}
Now {tex}\frac{{87 + 92 + 94 + 95 + x}}{5} \geq 90{/tex} {tex} \Rightarrow \frac{{368 + x}}{5} \geq 90{/tex}
Multiplying both sides by 5, we have
{tex}368 + x \geq 450 {/tex}
{tex}\Rightarrow x \geq 450 – 368{/tex}
{tex} \Rightarrow x \geq 82{/tex}
Thus the minimum marks needed to be obtained by Sunita = 82. - Let D (x, y, z) be the fourth vertex of parallelogram ABCD.
We know that diagonals of a parallelogram bisect each other. So the mid points of AC and BD coincide.
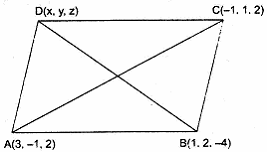
{tex}\therefore{/tex} Coordinates of mid point of AC {tex}\left( {\frac{{3 – 1}}{2},\;\frac{{ – 1 + 1}}{2},\;\frac{{2 + 2}}{2}} \right){/tex}
= (1, 0, 2)
Also coordinates of mid point of BD {tex}\left( {\frac{{x + 1}}{2},\;\frac{{y + 2}}{2},\;\frac{{z – 4}}{2}} \right){/tex}
{tex}\therefore{/tex} {tex}\frac{{x + 1}}{2} = 1{/tex} {tex}\Rightarrow{/tex} x + 1 = 2 {tex}\Rightarrow{/tex} x = 1
{tex}\frac{{y + 2}}{2} = 0{/tex} {tex}\Rightarrow{/tex} y + 2= 0 {tex}\Rightarrow{/tex} y = -2
{tex}\frac{{z – 4}}{2} = 2{/tex} {tex}\Rightarrow{/tex} z – 4 = 4 {tex}\Rightarrow{/tex} z = 8
Thus the coordinates of point D are (1, -2, 8)OR
To prove: Points P, Q, R, S forms a rectangle.
Formula: The distance between two points (x1, y1, z1) and (x2, y2, z2) is given by
D = {tex}\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}+\left(z_{2}-z_{1}\right)^{2}}{/tex}
Here,
(x1, y1, z1) = (2, 3, 5)
(x2, y2, z2) = (-4, 7, -7)
(x3, y3, z3) = (-2, 1, -10)
(x4, y4, z4) = (4, -3, 2)
Length PQ = {tex}\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}+\left(z_{2}-z_{1}\right)^{2}}{/tex}
{tex}=\sqrt{(-4-2)^{2}+(7-3)^{2}+(-7-5)^{2}}{/tex}
{tex}=\sqrt{(-6)^{2}+(4)^{2}+(-12)^{2}}{/tex}
{tex}=\sqrt{36+16+144}{/tex}
Length PQ {tex}=\sqrt{196}{/tex}
Length QR = {tex}\sqrt{\left(x_{3}-x_{2}\right)^{2}+\left(y_{3}-y_{2}\right)^{2}+\left(z_{3}-z_{2}\right)^{2}}{/tex}
{tex}=\sqrt{(-2+4)^{2}+(1-7)^{2}+(-10+7)^{2}}{/tex}
{tex}=\sqrt{(2)^{2}+(-6)^{2}+(-3)^{2}}{/tex}
{tex}=\sqrt{4+36+9}{/tex}
Length QR {tex}=\sqrt{49}{/tex}
Length RS = {tex}\sqrt{\left(x_{4}-x_{3}\right)^{2}+\left(y_{4}-y_{3}\right)^{2}+\left(z_{4}-z_{3}\right)^{2}}{/tex}
{tex}=\sqrt{(4+2)^{2}+(-3-1)^{2}+(2+10)^{2}}{/tex}
{tex}=\sqrt{(6)^{2}+(-4)^{2}+(12)^{2}}{/tex}
{tex}=\sqrt{36+16+144}{/tex}
Length RS {tex}=\sqrt{196}{/tex}
Length PS = {tex}\sqrt{\left(x_{4}-x_{1}\right)^{2}+\left(y_{4}-y_{1}\right)^{2}+\left(z_{4}-z_{1}\right)^{2}}{/tex}
{tex}=\sqrt{(4-2)^{2}+(-3-3)^{2}+(2-5)^{2}}{/tex}
{tex}=\sqrt{(2)^{2}+(-6)^{2}+(-3)^{2}}{/tex}
{tex}=\sqrt{4+36+9}{/tex}
Length PS {tex}=\sqrt{49}{/tex}
Length PR = {tex}\sqrt{\left(x_{3}-x_{1}\right)^{2}+\left(y_{3}-y_{1}\right)^{2}+\left(z_{3}-z_{1}\right)^{2}}{/tex}
{tex}=\sqrt{(-2-2)^{2}+(1-3)^{2}+(-10-5)^{2}}{/tex}
{tex}=\sqrt{(-4)^{2}+(-2)^{2}+(-15)^{2}}{/tex}
{tex}=\sqrt{16+4+225}{/tex}
Length PR {tex}=\sqrt{245}{/tex}
Length QS = {tex}\sqrt{\left(x_{4}-x_{2}\right)^{2}+\left(y_{4}-y_{2}\right)^{2}+\left(z_{4}-z_{2}\right)^{2}}{/tex}
{tex}=\sqrt{(4+4)^{2}+(-3-7)^{2}+(2+7)^{2}}{/tex}
{tex}=\sqrt{(8)^{2}+(-10)^{2}+(9)^{2}}{/tex}
{tex}=\sqrt{64+100+81}{/tex}
Length QS {tex}=\sqrt{245}{/tex}
Here, PQ = RS which are opposite sides of the polygon.
QR = PS which are opposite sides of the polygon.
Also the diagonals PR = QS.
Hence, the polygon is a rectangle. - To find: Expension of {tex}(\sqrt[3]{x}-\sqrt[3]{y})^{6}{/tex} by means of binomial theorem..
Formula used: {tex}^{n} C_{r}=\frac{n !}{(n-r) !(r) !}{/tex}
(a + b)n = {tex}^{n} C_{0} a^{n}+^{n} C_{1} a^{n-1} b+^{n} C_{2} a^{n-2} b^{2}{/tex}{tex}+\ldots \ldots+^{n} C_{n-1} a b^{n-1}+n C_{n} b^{n}{/tex}
We have, {tex}(\sqrt[3]{x}-\sqrt[3]{y})^{6}{/tex}
We can write {tex}\sqrt[3]{x}{/tex}, as {tex}x^{\frac{1}{3}}{/tex}, and {tex}\sqrt[3]{y}{/tex} , as {tex}y^{\frac{1}{3}}{/tex},
Now, we have to solve for {tex}\left(x^{\frac{1}{3}}-y^{\frac{1}{3}}\right)^{6}{/tex}
{tex}\Rightarrow\left[6 \mathrm{C}_{0}\left(\mathrm{x}^{\frac{1}{3}}\right)^{6-0}\right]+\left[6 \mathrm{C}_{1}\left(\mathrm{x}^{\frac{1}{3}}\right)^{6-1}\left(-\mathrm{y}^{\frac{1}{3}}\right)^{1}\right]{/tex}{tex}+\left[6 \mathrm{C}_{2}\left(\mathrm{x}^{\frac{1}{3}}\right)^{6-2}\left(-\mathrm{y}^{\frac{1}{3}}\right)^{2}\right]+\left[6 C_{3}\left(x^{\frac{1}{3}}\right)^{6-3}\left(-y^{\frac{1}{3}}\right)^{3}\right]{/tex}
{tex}+\left[6 \mathrm{C}_{4}\left(\mathrm{x}^{\frac{1}{3}}\right)^{6-4}\left(-\mathrm{y}^{\frac{1}{3}}\right)^{4}\right]+\left[6 \mathrm{C}_{5}\left(\mathrm{x}^{\frac{1}{3}}\right)^{6-5}\left(-\mathrm{y}^{\frac{1}{3}}\right)^{5}\right]{/tex}{tex}+\left[6 C_{6}\left(-y^{\frac{1}{3}}\right)^{6}\right]{/tex}
{tex}\Rightarrow\left[^{6} \mathrm{C}_{0}\left(\frac{^{6}}{x^{3}}\right)\right]-\left[^{6} \mathrm{C}_{1}\left(x^{\frac{5}{3}}\right)\left(y^{\frac{1}{3}}\right)\right]{/tex}{tex}+\left[6 \mathrm{C}_{2}\left(\mathrm{x}^{\frac{4}{3}}\right)\left(\mathrm{y}^{\frac{2}{3}}\right)\right]-\left[6 \mathrm{C}_{3}\left(\mathrm{x}^{\frac{3}{3}}\right)\left(\mathrm{y}^{\frac{3}{3}}\right)\right]{/tex}
{tex}+\left[^{6} \mathrm{C}_{4}\left(\mathrm{x}^{\frac{2}{3}}\right)\left(\mathrm{y}^{\frac{4}{3}}\right)\right]-\left[6 \mathrm{C}_{5}\left(\mathrm{x}^{\frac{1}{3}}\right)\left(\mathrm{y}^{\frac{5}{3}}\right)\right]{/tex}{tex}+\left[6 C_{6}\left(\frac{6}{y^{3}}\right)\right]{/tex}
{tex}\Rightarrow\left[\frac{6 !}{0 !(6-0) !}\left(x^{2}\right)\right]-\left[\frac{6 !}{1 !(6-1) !}\left(x^{\frac{5}{3}}\right)\left(y^{\frac{2}{3}}\right)\right]{/tex}{tex}+\left[\frac{6 !}{2 !(6-2) !}\left(x^{\frac{4}{2}}\right)\left(x^{\frac{2}{3}}\right)\right]{/tex}
{tex}-\left[\frac{6 !}{3 !(6-3) !}(x)(y)\right]+\left[\frac{6 !}{4 !(6-4) !}\left(x^{\frac{2}{3}}\right)\left(y^{\frac{4}{5}}\right)\right]{/tex}{tex}-\left[\frac{6 !}{5 !(6-5) !}\left(x^{\frac{1}{3}}\right)\left(y^{\frac{5}{3}}\right)\right]{/tex}{tex}+\left[\frac{6 !}{6 !(6-6) !}\left(y^{2}\right)\right]{/tex}
{tex}\Rightarrow\left[1\left(x^{2}\right)\right]-\left[6\left(x^{\frac{5}{3}}\right)\left(y^{\frac{1}{3}}\right)\right]+\left[15\left(x^{\frac{4}{3}}\right)\left(y^{\frac{2}{3}}\right)\right]{/tex}{tex}-[20(x)(y)]+\left[15\left(x^{\frac{2}{3}}\right)\left(\frac{4}{y^{3}}\right)\right]{/tex}
{tex}-\left[6\left(x^{\frac{1}{3}}\right)\left(y^{\frac{5}{3}}\right)\right]+\left[1\left(y^{2}\right)\right]{/tex}
{tex}\Rightarrow x^{2}-6 x^{\frac{5}{2}} y^{\frac{1}{3}}+15 x^{\frac{4}{3}} y^{\frac{2}{3}}-20 x y{/tex}{tex}+15 x^{\frac{2}{3}} y^{\frac{4}{3}}-6 x^{\frac{1}{3}} y^{\frac{5}{3}}+y^{2}{/tex}
Hence the result.OR
As discussed in the previous example, the middle term in the expansion of (1 + x)2n is given by {tex}T_{n+1}=\;^{2 n} C_{n} x^{n}{/tex}
So, the coefficient of the middle term in the expansion of (1 + x)2n is {tex}^{2 n} \mathrm{C}_{n}{/tex}.
Now, consider the expansion of (1 + x)2n-1 Here, the index (2n-1) is odd.
So, {tex}\left(\frac{(2 n-1)+1}{2}\right)^{t h}{/tex} and {tex}\left(\frac{(2 n-1)+1}{2}+1\right)^{\text { th }}{/tex}i.e., nth and (n + 1)th terms are middle terms.
Now, {tex}T_{n}=T_{(n-1)+1}{/tex},= {tex}^{2 n-1} C_{n-1}(1)^{(2 n-1)-(n-1)} x^{n-1}{/tex} = {tex}^{2 n-1} C_{n-1} x^{n-1}{/tex}
and, Tn+1 = {tex}^{2 n-1} C_{n}(1)^{(2 n-1)-n} x^{n}=\; ^{2 n-1}C_{n} x^{n}{/tex}
So, the coefficients of two middle terms in the expansion of (1 + x)2n-1 are {tex}^{2 n-1} C_{n-1}{/tex} and {tex}^{2n-1}{C_{n}}{/tex}.
{tex}\therefore{/tex} Sum of these coefficients = {tex}^{2 n-1} C_{n-1}+^{2 n-1} C_{n}{/tex}
= {tex}^{(2 n-1)+1}{C_{n}}{/tex} [{tex}\because{/tex} {tex}^{n} C_{r-1}+^{n} C_{r}=^{n+1} C_{r}{/tex}] = {tex}^{2 n} C_{n}{/tex}
= Coefficient of middle term in the expansion of (1 + x)2n. - Let x + yi {tex} = \sqrt { – 8 – 6i} {/tex}
Squaring both sides, we get
x2 – y2 + 2x yi = -8 – 6i
Equating the real and imaginary parts
x2 – y2 = -8…..(i)
and 2xy = -6
{tex}\therefore xy = – 3{/tex}
Now using the identity
(x2 + y2)2 = (x2 – y2)2 + 4x2y2
= (-82 + 4(-3)2
= 64 + 36 = 100
{tex}\therefore {x^2} + {y^2} = 10{/tex} ….. (ii) [Neglecting (-) sign as x2 + y2 > 0] Solving (i) and (ii) we get
x2 = 1 and y2 = 9
{tex}\therefore x = \pm 1{/tex} and {tex}y = \pm 3{/tex}
Since the sign of xy is negative
{tex}\therefore {/tex} if x = 1, y = -3
and if x = -1, y = 3{tex}\therefore \sqrt { – 8 – 6i} = \pm (1 – 3i){/tex}OR
(x + iy)(3 – 2i) = (12 + 5i)
==> x(3 – 2i) + iy(3 – 2i) = 12 + 5i
{tex}\Rightarrow{/tex} 3x – 2ix + 3iy – 2i2y = 12 + 5i
{tex}\Rightarrow{/tex} 3x + i(-2x + 3y) – 2(-1)y = 12 + 5i [{tex}\because{/tex} i2 = -1] {tex}\Rightarrow{/tex} 3x + i(-2x + 3y) + 2y = 12 + 5i
{tex}\Rightarrow{/tex} (3x + 2y) + i(-2x + 3y) = 12 + 5i
Comparing the real parts and the imaginary parts, we get
3x + 2y = 12 …(i)
-2x + 3y = 5 …(ii)
Solving eq. (i) and (ii) to find the value of x and y
Multiply eq. (i) by 2 and eq. (ii) by 3, we get
6x + 4y = 24 …(iii)
-6x + 9y = 15 …(iv)
Adding eq. (iii) and (iv), we get
6x + 4y – 6x + 9y = 24 + 15
{tex}\Rightarrow{/tex} 13y = 39
{tex}\Rightarrow{/tex} y = 3
Putting the value of y = 3 in eq. (i), we get
3x + 2(3) = 12
{tex}\Rightarrow{/tex} 3x + 6 = 12
{tex}\Rightarrow{/tex} 3x = 12 – 6
{tex}\Rightarrow{/tex} 3x = 6
{tex}\Rightarrow{/tex} x = 2
Hence, the value of x = 2 and y = 3 - We know that {tex}A = A \cap (A \cup B){/tex} and {tex}A = A \cup (A \cap B){/tex}
Now {tex}A \cap B = A \cap C{/tex} and {tex}A \cup B = A \cup C{/tex}
{tex}\therefore B = B \cup (B \cap A) = B \cup (A \cap B) = B \cup (A \cap C){/tex} {tex}[\because \,A \cap B = A \cap C]{/tex}
{tex} = (B \cup A) \cap (B \cup C){/tex} (By distributive law)
{tex} = (A \cup C) \cap (B \cup C){/tex}
{tex} = (A \cup C) \cap (B \cup C){/tex} {tex}[\because \,A \cup B = A \cup C]{/tex}
{tex} = (C \cup A) \cap (C \cup B){/tex}
{tex}= C \cup (A \cap B){/tex} (by distributive law)
{tex} = C \cup (A \cap C){/tex} {tex}[\because \,A \cap B = A \cap C]{/tex}
{tex} = C \cup (C \cap A) = C{/tex}
Hence B = C. Class 11 Maths Sample Paper Solution Section D
- Given that one urn contains two black balls and one white ball and second urn contains one black ball and two white balls as expressed in the figure below
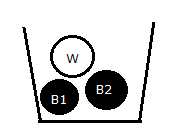
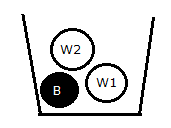
It is also given that one of the two urns is chosen, then a ball is randomly chosen from the urn, then second ball is chosen at random from the same urn without replacing the first ball and this condition can also be treated as taking out two balls at a time from one of the two urns. So,- Sample Space S = {B1B2, B1W, B2W, B2B1, WB1, WB2, W1W2, W1B, W2B, W2W1, BW1, BW2}
Total number of sample space = 12 - If two black balls are chosen
Total outcomes = 12
Favourable outcomes are B1B2, B2B1
{tex}\therefore{/tex} Total favourable outcomes = 2
We know that,
Probabiltiy {tex}=\frac{\text { Number of favourable outcomes }}{\text { Total number of outcomes }}{/tex}
{tex}\therefore{/tex} Required probability = {tex}\frac{2}{12}=\frac{1}{6}{/tex} - If two balls of opposite colours are chosen i.e. one black and one white
Favourable outcomes are B1W, B2W, WB1, WB2, W1B, W2B, BW1, BW2
{tex}\therefore{/tex} Total favourable outcomes = 8 and Total outcomes = 12
We know that,
Probabiltiy {tex}=\frac{\text { Number of favourable outcomes }}{\text { Total number of outcomes }}{/tex}
{tex}\therefore{/tex} Required probability = {tex}\frac{8}{12}=\frac{2}{3}{/tex}
- Sample Space S = {B1B2, B1W, B2W, B2B1, WB1, WB2, W1W2, W1B, W2B, W2W1, BW1, BW2}
- Clearly,
cos x cos 2x cos 3x = {tex}\frac{1}{2}{/tex} {2 cos x cos 2x cos 3x}
= {tex}\frac{1}{2}{/tex} {(2 cos x cos 2x) cos 3x}
= {tex}\frac{1}{2}{/tex} {(cos 3x + cosx) cos 3x}
= {tex}\frac{1}{2}{/tex} {cos2 3x + cos 3x cos x}
= {tex}\frac{1}{4}{/tex} {2 cos2 3x + 2 cos 3x cos x}
= {tex}\frac{1}{4}{/tex} {1 + cos 6x + cos 4x + cos 2x}
{tex}\therefore{/tex} {tex}\mathop {\lim }\limits_{x \to 0} \,\frac{{1 – \cos \,x\,\cos \,2x\cos \,3x}}{{{{\sin }^2}2x}}{/tex}
= {tex}\mathop {\lim }\limits_{x \to 0} \frac{{1 – \frac{1}{4}(1 + \cos 6x + \cos 4x + \cos 2x)}}{{{{\sin }^2}2x}}{/tex}
= {tex}\mathop {\lim }\limits_{x \to 0} \frac{{4 – 1 – \cos 6x – \cos 4x – \cos 2x}}{{4{{\sin }^2}2x}}{/tex}
= {tex}\mathop {\lim }\limits_{x \to 0} \frac{{(1 – \cos 6x) + (1 – \cos 4x) + (1 – \cos 2x)}}{{4{{\sin }^2}2x}}{/tex}
= {tex}\mathop {\lim }\limits_{x \to 0} \frac{{2{{\sin }^2}3x + 2{{\sin }^2}2x + 2{{\sin }^2}x}}{{4{{\sin }^2}2x}}{/tex}
= {tex}\mathop {\lim }\limits_{x \to 0} \frac{{\frac{{{{\sin }^2}3x}}{{{x^2}}} + \frac{{{{\sin }^2}2x}}{{{x^2}}} + \frac{{{{\sin }^2}x}}{{{x^2}}}}}{{2\left( {\frac{{{{\sin }^2}2x}}{{{x^2}}}} \right)}}{/tex}
= {tex}\mathop {\lim }\limits_{x \to 0} \frac{{{{\left( {\frac{{\sin 3x}}{x}} \right)}^2} + {{\left( {\frac{{\sin 2x}}{x}} \right)}^2} + {{\left( {\frac{{\sin x}}{x}} \right)}^2}}}{{2{{\left( {\frac{{\sin 2x}}{x}} \right)}^2}}}{/tex}
= {tex}\mathop {\lim }\limits_{x \to 0} \frac{{9 \times {{\left( {\frac{{\sin 3x}}{{3x}}} \right)}^2} + 4 \times {{\left( {\frac{{\sin 2x}}{{2x}}} \right)}^2} + {{\left( {\frac{{\sin x}}{x}} \right)}^2}}}{{2 \times 4{{\left( {\frac{{\sin 2x}}{{2x}}} \right)}^2}}}{/tex}
= {tex}\frac{9 \times 1+4 \times 1+1}{8}=\frac{14}{8}=\frac{7}{4}{/tex}OR
- {tex}f(x) = \left\{ {\begin{array}{*{20}{c}} {|x| + 1,}&{x < 0} \\ {0,}&{x = 0} \\ {|x| – 1,}&{x > 0} \end{array}} \right.{/tex}
At x = 0,
RHL {tex} = \mathop {\lim }\limits_{x \to {0^ + }} f(x) = \mathop {\lim }\limits_{h \to 0} f(0 + h){/tex}
{tex} = \mathop {\lim }\limits_{h \to 0} |0 + h| – 1{/tex}
= – 1
LHL {tex} = \mathop {\lim }\limits_{h \to {0^ – }} f(x) = \mathop {\lim }\limits_{h \to 0} f|0 – h|{/tex}
{tex} = \mathop {\lim }\limits_{h \to 0} |0 – h| + 1{/tex}
{tex} = \mathop {\lim }\limits_{h \to 0} – (0 – h) + 1{/tex}
{tex} = \mathop {\lim }\limits_{h \to 0} h + 1{/tex}
= 0 + 1 = 1
{tex}\Rightarrow{/tex} RHL {tex} \ne {/tex} LHL
{tex}\Rightarrow{/tex} At x = 0, limi does not exist.
Hence, {tex}\mathop {\lim }\limits_{x \to a} f(x){/tex} exists for all a {tex} \ne {/tex} 0. - Let {tex}f ( x ) = \cos \left( x – \frac { \pi } { 8 } \right){/tex}
By using first principle of derivative
We have,
{tex}{f^\prime }(x) = \mathop {\lim }\limits_{h \to 0} \frac{{f(x + h) – f(x)}}{h}{/tex}
{tex} \Rightarrow {f^\prime }(x) = \mathop {\lim }\limits_{h \to 0} \frac{{\cos \left( {x + h – \frac{\pi }{8}} \right) – \cos \left( {x – \frac{\pi }{8}} \right)}}{b}{/tex}{tex}\left[ \because f ( x ) = \cos \left( x – \frac { \pi } { 8 } \right) \right]{/tex}
{tex} = \mathop {\lim }\limits_{h \to 0} \frac{{ – 2\sin \left( {\frac{{x + h – \frac{\pi }{8} + x – \frac{\pi }{8})}}{2}} \right)\sin \left( {\frac{{x + h – \frac{\pi }{8} – x + \frac{\pi }{8}}}{2}} \right)}}{h}{/tex}
{tex}\left[ {\because \cos C – \cos D = – 2\sin \left( {\frac{{C + D}}{2}} \right)\sin \left( {\frac{{C – D}}{2}} \right)} \right]{/tex}
{tex} = \mathop {\lim }\limits_{h \to 0} \frac{{ – 2\sin \frac{{2x – 2\left( {\frac{\pi }{8}} \right) + h}}{2}}}{{2 \times \frac{h}{2}}}{/tex}
{tex} = – \sin \frac{{2x – 2\left( {\frac{\pi }{8}} \right) + 0}}{2} \times 1{/tex}{tex}\left[ {\therefore \mathop {\lim }\limits_{x \to 0} \frac{{\sin \frac{h}{2}}}{{\frac{h}{2}}} = 1} \right]{/tex}
{tex}= – \sin \frac { 2 \left( x – \frac { \pi } { 8 } \right) } { 2 }{/tex}
{tex} \Rightarrow {f^\prime }(x) = – \sin \left( {x – \frac{\pi }{8}} \right){/tex}
- {tex}f(x) = \left\{ {\begin{array}{*{20}{c}} {|x| + 1,}&{x < 0} \\ {0,}&{x = 0} \\ {|x| – 1,}&{x > 0} \end{array}} \right.{/tex}
- Let the edges of rectangular block in GP be a, ar and ar2, respectively…. (i)
Now, Volume =216 cm3
{tex}\Rightarrow{/tex} a(ar) (ar2) = 216 [{tex}\because{/tex} volume of cuboid = l {tex}\times{/tex} b {tex}\times{/tex} h] {tex}\Rightarrow{/tex} (ar)3 = (6)3
{tex}\Rightarrow{/tex} ar = 6 cm [taking cube root] …(ii)
and total surface area = 252 cm
{tex}\Rightarrow{/tex} 2[a (ar) + ar (ar2) + a (ar2)] = 252 [{tex}\because{/tex} sufrace area of cuboid = 2 (lb + bh + hl)] From Eq. (ii), we get
2 (6a +36r +36) = 252
{tex}\Rightarrow{/tex} 12 (a + 6r + 6) = 252
{tex}\Rightarrow{/tex} a + 6r = 15 [divide both sides by 12] …(iii)
{tex}\Rightarrow{/tex} a + 6 {tex}\times{/tex} {tex}\left( \frac { 6 } { a } \right){/tex} = 15 [from Eq. (ii)] {tex}\Rightarrow{/tex} a2 – 15a + 36 = 0 {tex}\Rightarrow{/tex} (a – 12) (a – 3) = 0
{tex}\Rightarrow{/tex} a = 3, 12
From Eq. (iii), we get
When a = 3, then 3 + 6r = 15 {tex}\Rightarrow{/tex} r = 2
and when a = 12, then 12 + 6r = 15 {tex}\Rightarrow{/tex} r = {tex}\frac { 1 } { 2 }{/tex}
On putting above values in Eq. (i),
edges are 3, 3 {tex}\times{/tex} 2, 3 {tex}\times{/tex} (2)2 or 12, 12 {tex}\times{/tex} {tex}\left( \frac { 1 } { 2 } \right){/tex}, 12 {tex}\times{/tex} {tex}\left( \frac { 1 } { 2 } \right) ^ { 2 }{/tex}
i.e., 3, 6, 12 or 12, 6, 3.
Hence, the length of the longest edge is 12 cm. 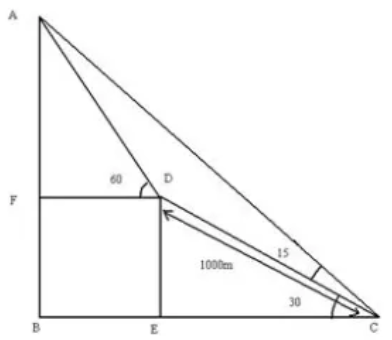
DE = 1000 sin 30 = 1000 {tex}\times{/tex} {tex}\frac{1}{2}{/tex} = 500 m = FB
EC = 1000 cos 30 = 1000 {tex}\times{/tex} {tex}\frac{\sqrt{3}}{2}{/tex} = 500{tex} \sqrt{3}{/tex} m
Let A F = x m
D F = {tex}\frac{x}{\sqrt{3}}{/tex} m = B E
We know,
From {tex}\triangle \mathrm{ABC}{/tex}
tan 45 = {tex} \frac{A B}{B C}{/tex}
{tex}\Rightarrow 1 = \frac{A F+F B}{B E+E C}{/tex}
{tex}\Rightarrow 1 = \frac{x+500}{\frac{x}{\sqrt{3}}+500 \sqrt{3}}{/tex}
{tex}\Rightarrow \frac{x}{\sqrt{3}}+500 \sqrt{3} = x+500{/tex}
{tex}\Rightarrow x+1500 = x \sqrt{3}+500 \sqrt{3}{/tex}
{tex}\Rightarrow 1500-500 \sqrt{3} = x \sqrt{3}-x{/tex}
{tex}\Rightarrow 500 \sqrt{3}(\sqrt{3}-1) = x(\sqrt{3}-1){/tex}
{tex}\therefore{/tex} x = 500{tex} \sqrt{3}{/tex} m
The height of the triangle is AB = AF + FB = 500({tex}\sqrt{3}{/tex} + 1) mOR
LHS = {tex}\left(\frac{1}{\sec ^{2} \theta-\cos ^{2} \theta}+\frac{1}{\csc ^{2} \theta-\sin ^{2} \theta}\right){/tex}sin2{tex}\theta{/tex} cos2{tex}\theta{/tex}
= {tex}\left(\frac{1}{\frac{1}{\cos ^{2} \theta}-\cos ^{2} \theta}+\frac{1}{\left(\frac{1}{\sin ^{2} \theta}-\sin ^{2} \theta\right)}\right){/tex}sin2{tex}\theta{/tex} cos2{tex}\theta{/tex}
= {tex}\left(\frac{1}{\frac{1-\cos ^{4} \theta}{\cos ^{2} \theta}}+\frac{1}{\frac{1-\sin ^{4} \theta}{\sin ^{2} \theta}}\right){/tex} sin2{tex}\theta{/tex} cos2{tex}\theta{/tex}
= {tex}\left(\frac{\cos ^{2} \theta}{\left(1-\cos ^{2} \theta\right)\left(1+\cos ^{2} \theta\right)}+\frac{\sin ^{2} \theta}{\left(1-\sin ^{2} \theta\right)\left(1+\sin ^{2} \theta\right)}\right){/tex} sin2{tex}\theta{/tex} cos2{tex}\theta{/tex} ({tex}\because{/tex}1 − a4 = 1 − (a2)2 = (1 − a2) (1 + a2))
= {tex}\left( {\frac{{{{\cos }^2}\theta }}{{{{\sin }^2}\theta \left( {1 + {{\cos }^2}\theta } \right)}} + \frac{{{{\sin }^2}\theta }}{{{{\cos }^2}\theta \left( {1 + {{\sin }^2}} \right)}}} \right){/tex}sin2{tex}\theta{/tex} cos2{tex}\theta{/tex} ({tex}\because{/tex} 1 − cos2{tex}\theta{/tex} = sin2{tex}\theta{/tex} and 1 − sin2{tex}\theta{/tex} = cos2{tex}\theta{/tex})
= {tex}\left(\frac{\cos ^{4} \theta\left(1+\sin ^{2} \theta\right)+\sin ^{4} \theta\left(1+\cos ^{2} \theta\right)}{\sin ^{2} \theta \cos ^{2} \theta\left(1+\cos ^{2} \theta\right)\left(1+\sin ^{2} \theta\right)}\right){/tex}sin2{tex}\theta{/tex} cos2{tex}\theta{/tex}
= {tex}\frac{\cos ^{4} \theta+\sin ^{2} \theta \cos ^{4} \theta+\sin ^{4} \theta+\cos ^{2} \theta \sin ^{4} \theta}{\left(1+\cos ^{2} \theta\right)\left(1+\sin ^{2} \theta\right)}{/tex}
= {tex}\frac{\left(\cos ^{2} \theta\right)^{2}+\left(\sin ^{2} \theta\right)^{2}+2 \cos ^{2} \theta \sin ^{2} \theta-2 \cos ^{2} \theta \sin ^{2} \theta+\sin ^{2} \theta \cos ^{4} \theta+\cos ^{2} \theta \sin ^{4} \theta}{\left(1+\cos ^{2} \theta\right)\left(1+\sin ^{2} \theta\right)}{/tex} (adding and subtracting 2 cos2{tex}\theta{/tex} sin2{tex}\theta{/tex} )
= {tex}\frac{\left(\cos ^{2} \theta+\sin ^{2} \theta\right)^{2}-2 \cos ^{2} \theta \sin ^{2} \theta+\sin ^{2} \theta \cos ^{2} \theta\left(\cos ^{2} \theta+\sin ^{2} \theta\right)}{1+\sin ^{2} \theta+\cos ^{2} \theta+\sin ^{2} \theta \cos ^{2} \theta}{/tex}
= {tex}\frac{1^{2}-2 \cos ^{2} \theta \sin ^{2} \theta+\sin ^{2} \theta \cos ^{2} \theta \cdot 1}{1+1+\sin ^{2} \theta \cos ^{2} \theta}{/tex}
= {tex}\frac{1-\sin ^{2} \theta \cos ^{2} \theta}{2+\sin ^{2} \theta \cos ^{2} \theta}{/tex}
= RHS
Hence proved.Class 11 Maths Sample Paper Solution Section E
- Given curve is a parabola
Equation of parabola is x2 = 4ay
It passes through the point (6, 4.5)
{tex}\Rightarrow {/tex} 36 = 4 {tex}\times{/tex} a {tex}\times{/tex} 4.5
{tex}\Rightarrow {/tex} 36 = 18a
{tex}\Rightarrow {/tex} a = 2
Equation of parabola is x2 = 8y - Distance between focus and vertex is = a = {tex}\sqrt{(4-4)^2+(5-3)^2}{/tex} = 2
Equation of parabola is (y – k)2 = 4a(x – h)
where (h, k) is vertex
{tex}\Rightarrow{/tex} Equation of parabola with vertex (3, 4) & a = 2
{tex}\Rightarrow{/tex} (y – 4)2 = 8(x – 3) - Equation of parabola with axis along x – axis
y2 = 4ax
which passes through (2, 3)
{tex}\Rightarrow{/tex} 9 = 4a {tex}\times{/tex} 2
{tex}\Rightarrow{/tex} 4a = {tex}\frac92{/tex}
hence required equation of parabola is
{tex}y^2=\frac{9}{2} x{/tex}
{tex}\Rightarrow{/tex} 2y2 = 9x
Hence length of latus rectum = 4a = 4.5 OR
x2 = 8y
a = 2
Focus of parabola is (0, 2)
length of latus rectum is 4a = 4 {tex}\times{/tex} 2 =8
Equation of directrix y + 2 =0
- Given curve is a parabola
- By using formula,{tex}{\sigma ^2} = \frac{1}{N}\left[ {\sum\limits_{i = 1}^n {{f_i}} {{\left( {{x_i} – \bar x} \right)}^2}} \right]{/tex}
xi fi fixi xi – {tex}\overline x{/tex} (xi – {tex}\overline x{/tex})2 fi(xi – {tex}\overline x{/tex})2 4 3 12 -10 100 {tex}300{/tex} 8 5 40 -6 36 {tex}180{/tex} 11 9 99 -3 9 {tex}81{/tex} 17 5 85 3 9 {tex}45{/tex} 20 4 80 6 36 {tex}144{/tex} 24 3 72 10 100 {tex}300{/tex} 32 1 32 18 324 {tex}324{/tex} Total 30 420 {tex}1374{/tex} Given, N = {tex}\sum f_i{/tex} = 30, {tex}\sum f_ix_i{/tex} = 420 and {tex}\sum f_{i}\left(x_{i}-\overline{x}\right)^{2}{/tex} = 1374
{tex}\therefore{/tex} {tex}\bar x = \frac{{\sum\limits_{i = 1}^7 {{f_i}} {x_i}}}{N}{/tex} = {tex}\frac{420}{30}{/tex} = 14
Variance ({tex}\sigma^2{/tex}) = {tex}\frac{1}{N}\sum\limits_{i = 1}^7 {{f_i}} {\left( {{x_i} – \bar x} \right)^2}{/tex} = {tex}\frac{1}{30}{/tex} {tex}\times{/tex} {tex}1374 = 45.8{/tex}
Standard deviation, {tex}\sigma{/tex} = {tex}\sqrt{\sigma^2}{/tex} = {tex}\sqrt{45.8}{/tex} = 6.77 - Variance ({tex}\sigma^2{/tex}) = {tex}\frac{1}{N}\sum\limits_{i = 1}^7 {{f_i}} {\left( {{x_i} – \bar x} \right)^2}{/tex} = {tex}\frac{1}{30}{/tex} {tex}\times{/tex} {tex}1374 = 45.8{/tex}
- Given, N = {tex}\sum f_i{/tex} = 30, {tex}\sum f_ix_i{/tex} = 420 and {tex}\sum f_{i}\left(x_{i}-\overline{x}\right)^{2}{/tex} = 1374
{tex}\therefore{/tex} {tex}\bar x = \frac{{\sum\limits_{i = 1}^7 {{f_i}} {x_i}}}{N}{/tex} = {tex}\frac{420}{30}{/tex} = 14 OR
{tex}\sigma^{2}=\frac{1}{N} \Sigma\left(x_{i}-\bar{x}\right){/tex}
To practice more questions & prepare well for exams, download myCBSEguide App. It provides complete study material for CBSE, NCERT, JEE (main), NEET-UG and NDA exams. Teachers can use Examin8 App to create similar papers with their own name and logo.
- By using formula,{tex}{\sigma ^2} = \frac{1}{N}\left[ {\sum\limits_{i = 1}^n {{f_i}} {{\left( {{x_i} – \bar x} \right)}^2}} \right]{/tex}
- Since, at least 3 questions from each part have to be selected
Part I Part II 3 5 4 4 3 5 So number of ways are
3 questions from part I and 5 questions from part II can be selected in {tex}n^8 C_3 \times{ }^7 C_5{/tex} ways
4 questions from part I and 4 questions from part II can be selected in {tex}{ }^8 C_4 \times{ }^7 C_4{/tex} ways
5 questions from part I and 3 questions from part II can be selected in {tex}{ }^8 C_5 \times{ }^7 C_3{/tex} ways
So required number of ways are
{tex}{ }^8 C_3 \times{ }^7 C_5+{ }^8 C_4 \times{ }^7 C_4+{ }^8 C_5 \times{ }^7 C_3{/tex}
{tex}\Rightarrow \frac{8 !}{5 ! \times 3 !} \times \frac{7 !}{5 ! \times 2 !}+\frac{8 !}{4 ! \times 4 !} \times \frac{7 !}{4 ! \times 3 !}+\frac{8 !}{5 ! \times 3 !} \times \frac{7 !}{4 ! \times 3 !}{/tex}
{tex}\Rightarrow \frac{8 \times 7 \times 6}{3 \times 2 \times 1} \times \frac{7 \times 6}{2 \times 1}+\frac{8 \times 7 \times 6 \times 5}{4 \times 3 \times 2 \times 1} \times \frac{7 \times 6 \times 5}{3 \times 2 \times 1}+\frac{8 \times 7 \times 6}{3 \times 2 \times 1} \times \frac{7 \times 6 \times 5 \times 4}{4 \times 3 \times 2 \times 1}{/tex}
{tex}\Rightarrow{/tex} 56 {tex}\times{/tex} 21 + 70 {tex}\times{/tex} 35 + 56 {tex}\times{/tex} 35
{tex}\Rightarrow{/tex} 1344 + 2450 + 1960
{tex}\Rightarrow{/tex} 5754 - Ashish is selecting 3 questions from part I so he has to select remaining 5 questions from part II
The number of ways of selection is
3 questions from part I and 5 questions from part II can be selected in {tex}{ }^8 C_3 \times{ }^7 C_5{/tex} ways
{tex}\Rightarrow{ }^8 C_3 \times{ }^7 C_5{/tex}
{tex}\Rightarrow \frac{8 !}{5 ! \times 3 !} \times \frac{7 !}{5 ! \times 2 !}{/tex}
{tex}\Rightarrow \frac{8 \times 7 \times 6}{3 \times 2 \times 1} \times \frac{7 \times 6}{2 \times 1}{/tex}
{tex}\Rightarrow{/tex} 56 {tex}\times{/tex} 21
{tex}\Rightarrow{/tex} 1344
- Since, at least 3 questions from each part have to be selected
CBSE Sample Papers for Class 11 2024
- Physics
- Chemistry
- Mathematics
- Biology
- Accountancy
- Economics
- Business Studies
- Computer Science
- Informatics Practices
- English Core
- Hindi Core
- Hindi Elective
- History
- Political Science
- Geography
- Sociology
- Physical Education
- Other Subjects
To download sample paper for class 11 Physics, Chemistry, Biology, History, Political Science, Economics, Geography, Computer Science, Home Science, Accountancy, Business Studies and Home Science; do check myCBSEguide app or website. myCBSEguide provides sample papers with solution, test papers for chapter-wise practice, NCERT solutions, NCERT Exemplar solutions, quick revision notes for ready reference, CBSE guess papers and CBSE important question papers. Sample Paper all are made available through the best app for CBSE students and myCBSEguide website.

Test Generator
Create question paper PDF and online tests with your own name & logo in minutes.
Create Now
myCBSEguide
Question Bank, Mock Tests, Exam Papers, NCERT Solutions, Sample Papers, Notes
Install Now
This site is very good… all my paper questions came from this site. ?