1. Home
  2. /
  3. CBSE
  4. /
  5. Class 09
  6. /
  7. Mathematics
  8. /
  9. Class 9 Maths Sample...

Class 9 Maths Sample Paper 2023-24

by
myCBSEguide App

myCBSEguide App

Download the app to get CBSE Sample Papers 2023-24, NCERT Solutions (Revised), Most Important Questions, Previous Year Question Bank, Mock Tests, and Detailed Notes.

Install Now

CBSE class 9 Maths sample paper 2023-24 has both subjective and objective type questions. Especially you will find all case studies in subjective format. Unlike class 10 there is only one course in class 9 Mathematics. All students will study the same course content. You can download the model question paper for class 9 maths from myCBSEguide App or our student dashboard for free.

CBSE class 9 Maths Sample Paper 2022-23

Sample Paper of class 9 Math – in PDF

CBSE sample question papers (solved) class 9 Mathematics is released for session 2023-24.  CBSE, New Delhi has issued the new marking scheme and blueprint for Class 9 Mathematics. We are providing Mathematics guess papers for Class 9 annual examinations 2024. These sample question papers are available for free download in the myCBSEguide app and website in PDF format. CBSE Sample Papers for class 9 Mathematics with solutions will certainly help students to score high in exams.

The Best Model Papers for Class 9 Maths 2023-24

We know that CBSE issues model papers for board classes only. So, the model papers for classes 9th and 11th are prepared by schools only. In this case, the format and difficulty level of the question paper may vary from school to school.

That’s why it is very important that you should have a standard question paper with a moderate difficulty level. Here, the model papers provided by myCBSEguide app and website follow CBSE guidelines word to word. So, these are the best model papers for class 9th students.

Sample Papers of Class 9 Maths 2024 with solution

Download PDF 

CBSE Sample Papers Class 9 Mathematics

As discussed, CBSE does not conduct board exams for class 9 students. It is purely a home exam. But schools have to follow the guidelines issued by CBSE while preparing the question paper. It is necessary to assure uniformity in terms of difficulty level and format of the question paper.

In most cases, the CBSE examination portal provides question papers and schools download them from CBSE official website only.

Class 09 – Mathematics Sample Paper – 01 (2023-24)

Class 09 – Mathematics
Sample Paper – 01 (2023-24)

Maximum Marks: 80
Time Allowed: : 3 hours

General Instructions:

  1. This Question Paper has 5 Sections A-E.
  2. Section A has 20 MCQs carrying 1 mark each.
  3. Section B has 5 questions carrying 02 marks each.
  4. Section C has 6 questions carrying 03 marks each.
  5. Section D has 4 questions carrying 05 marks each.
  6. Section E has 3 case based integrated units of assessment (04 marks each) with subparts of the values of 1, 1 and 2 marks each respectively.
  7. All Questions are compulsory. However, an internal choice in 2 Qs of 5 marks, 2 Qs of 3 marks and 2 Questions of 2 marks has been provided. An internal choice has been provided in the 2marks questions of Section E.
  8. Draw neat figures wherever required. Take π =22/7 wherever required if not stated.

  1. Section A Class 9 Maths Sample Paper 2023-24

  2. The distance of the point (2,3) from the y-axis
    a) 5 units
    b) 3 units
    c) {tex}\sqrt {13} {/tex} units
    d) 2 units
  3. If the area of an equilateral triangle is {tex}36\sqrt 3 \;c{m^2}{/tex} , then the perimeter of the triangle is
    a) 18 cm
    b) {tex}12\sqrt 3 \;cm{/tex}
    c) 36 cm
    d) 12 cm
  4. In the given figure, AB is a diameter of the circle APBR. APQ and RBQ are straight lines. If {tex}\angle A = {35^o}{/tex} and , then the measure of {tex}\angle PBR{/tex} is

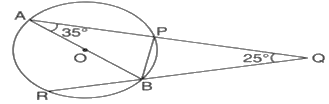    a) {tex}{155^o}{/tex}
    b) {tex}{135^o}{/tex}
    c) {tex}{165^o}{/tex}
    d) {tex}{115^o}{/tex}
  5. In fig D is mid-point of AB and DE {tex}\parallel{/tex} BC then AE is equal to

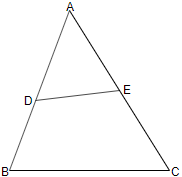    a) AD
    b) DB
    c) BC
    d) EC
  6. The value of x – yx-y when x = 2 and y = -2, is
    a) 14
    b) -18
    c) 18
    d) -14
  7. In Figure, if EC || AB, {tex}\angle{/tex}ECD = 70° and {tex}\angle{/tex}BDO = 20°, then {tex}\angle{/tex}OBD is

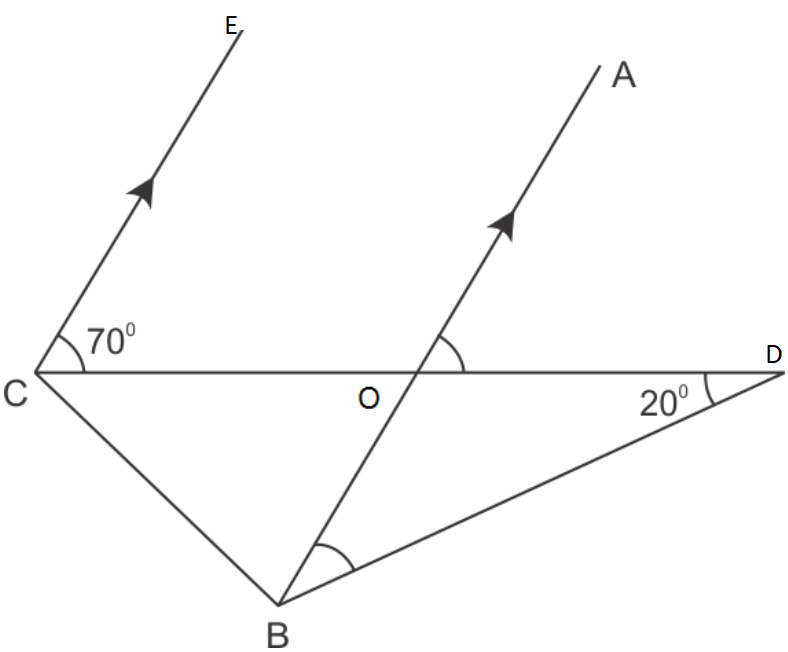    a) 50°
    b) 20°
    c) 60°
    d) 70°

    To practice more questions & prepare well for exams, download myCBSEguide App. It provides complete study material for CBSE, NCERT, JEE (main), NEET-UG and NDA exams. Teachers can use Examin8 App to create similar papers with their own name and logo.

  8. Express ‘x’ in terms of ‘y’ in the equation 2x – 3y – 5 = 0.
    a) {tex}x = \frac{{3y – 5}}{2}{/tex}
    b) {tex}x = \frac{{3y + 5}}{2}{/tex}
    c) {tex}x = \frac{{5 – 3y}}{2}{/tex}
    d) {tex}x = \frac{{3 + 5y}}{2}{/tex}
  9. If {tex}x+\frac{1}{x}=5{/tex}, then {tex}x^{2}+\frac{1}{x^{2}}={/tex}
    a) 23
    b) 27
    c) 25
    d) 10
  10. If {tex}\frac{3-\sqrt{5}}{3+2 \sqrt{5}}=a \sqrt{5}-\frac{19}{11} b{/tex} , then the value of b is
    a) 3
    b) 1
    c) -1
    d) 2
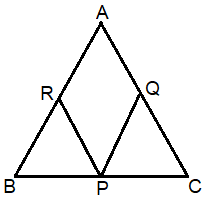
  11. In a {tex}\triangle{/tex}ABC, P, Q and R are the mid-points of the sides BC, CA and AB respectively. If AC = 21 cm, BC = 29 cm and AB = 30 cm, find the perimeter of the quadrilateral ARPQ?
    a)   20 cm
    b)  80 cm
    c)  51 cm
    d)   52 cm
  12. The value of x in 3 + 2x = {tex}(64)^{\frac{1}{2}}+(27)^{\frac{1}{3}}{/tex} is
    a) 14
    b) 8
    c) 5
    d) 3
  13. The equation x = 7 in two variables can be written as
    a) 1.x + 1.y = 7
    b) 1.x + 0.y = 7
    c) 0.x + 1.y = 7
    d) 0.x + 0.y = 7
  14. In the adjoining figure, the three lines AB, CD and EF all pass through the point O. If {tex}\angle {/tex}EOB = 90° and x:y = 2:1 then {tex} \angle {/tex}BOD and {tex}\angle {/tex}COE:-

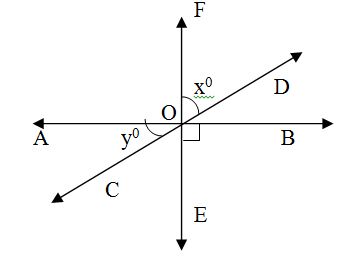    a) 60°, 60°
    b) 30°, 60°
    c) 80°, 20°
    d) 45°, 45°
  15. Rationalisation of the denominator of {tex}\frac{1}{\sqrt{5}+\sqrt{2}}{/tex} gives
    a) {tex}\sqrt{5}+\sqrt{2}{/tex}
    b) {tex}\sqrt{5}-\sqrt{2}{/tex}
    c) {tex}\frac{1}{\sqrt{10}}{/tex}
    d) {tex}\frac{\sqrt{5}-\sqrt{2}}{3}{/tex}
  16. In the given figure, if {tex}\angle BAC = {25^o}{/tex}, then {tex}\angle BOC{/tex} is equal to

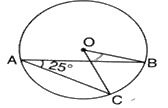    a) {tex}{50^o}{/tex}
    b) {tex}{125^o}{/tex}
    c) {tex}{25^o}{/tex}
    d) {tex}{60^o}{/tex}
  17. The perpendicular distance of a point Q(4, 7) from y-axis is
    a) 4 units
    b) 3 units
    c) 7 units
    d) 11 units
  18. If a linear equation has solutions (1, 2), (-1, -16) and (0, -7), then it is of the form
    a) y = 9x – 7
    b) 9x – y + 7 = 0
    c) x – 9y = 7
    d) x = 9y – 7
  19. If x + y + z = 0, then x3 + y3 + z3 is
    a) 3xyz
    b) xyz
    c) 2xyz
    d) 0
  20. Assertion (A): A parallelogram consists of two congruent triangles.
    Reason (R): Diagonal of a parallelogram divides it into two congruent triangles.

    a) Both A and R are true and R is the correct explanation of A.
    b) Both A and R are true but R is not the correct explanation of A.
    c) A is true but R is false.
    d) A is false but R is true.
  21. Assertion (A): If {tex}\sqrt{2}{/tex} = 1.414, {tex}\sqrt{3}{/tex} = 1.732, then {tex}\sqrt{5}=\sqrt{2}+\sqrt{3}{/tex}.
    Reason (R): Square root of a positive real number always exists.

    a) Both A and R are true and R is the correct explanation of A.
    b) Both A and R are true but R is not the correct explanation of A.
    c) A is true but R is false.
    d) A is false but R is true.

  22. Section B Class 9 Maths Sample Paper 2023-24

  23. In the given figure, we have X and Y are the mid-points of AC and BC and AX = CY. Show that AC = BC.
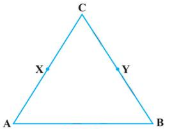
  24. If P, Q, and R are three points on a line and Q is between P and R, then prove that PR – QR = PQ.
  25. Name the quadrant in which the point lies :(i) A(1, 1) (ii) (–2, –4) (iii) C(1, –2).
  26. Express the number in decimal form: {tex}\frac{1}{9}{/tex}

    OR

    Simplify: {tex}\left(\frac{1}{3^{3}}\right)^{7}{/tex}

  27. The ratio of the volumes of the two cones is 4 : 5 and the ratio of the radii of their bases is 2 : 3. Find the ratio of their vertical heights.

    OR

    A cylinder and a cone have equal heights and equal radii of their bases. If their curved surface areas are in the ratio 8:5. Show that the ratio of radius to height of each is 3:4.

  28. Section C Class 9 Maths Sample Paper 2023-24

  29. If {tex}\sqrt{2}{/tex}=1.4142, find the value of {tex}\sqrt{\frac{\sqrt{2}-1}{\sqrt{2}+1}}.{/tex}
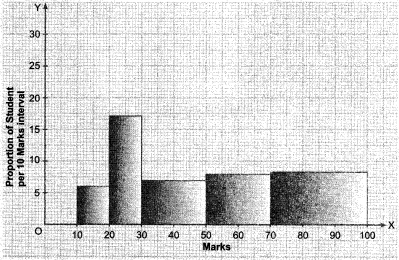
  30. The marks obtained (out of 100) by a class of 80 students are given below:
    Marks10-2020-3030-5050-7070-100
    Number of students617151626

    Construct a histogram to represent the data above.

  31. In Fig., AD is the median and DE || AB. Prove that BE is the median.
  32. Write linear equation 3x + 2y =18 in the form of ax + by + c = 0. Also write the values of a, b and c. Are (4, 3) and (1, 2) solution of this equation?
  33. The production of oil (in lakh tonnes) in some of the refineries in India during 1982 was given below:
    Refinery:BarauniKoyaliMathuraMumbaiFlorida
    Production of oil
    (in lakh tonnes)    		3070404525

    Construct a bar graph to represent the above data so that the bars are drawn horizontally.

    OR

    Draw a histogram to represent the following grouped frequency distribution:

    Ages (in years)Number of teacher
    20 – 2410
    25 – 2928
    30 – 3432
    35 – 3948
    40 – 4450
    45 – 4935
    50 – 5412
  34. Simplify the following expression: (x + y + z)2 + (x + {tex}\frac{y}{2}{/tex} + {tex}\frac{z}{3}{/tex})2 – ({tex}\frac{x}{2}{/tex} + {tex}\frac{y}{3}{/tex} + {tex}\frac{z}{4}{/tex})2

  35. Section D Class 9 Maths Sample Paper 2023-24

  36. In the given figure, AB || CD and CD || EF. Also, EA {tex}\perp{/tex} AB. If {tex}\angle{/tex}BEF = 45°, then find the values of x, y and z.

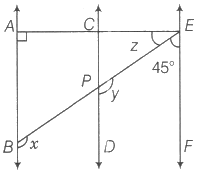
    OR

    In each of the figures given below, AB {tex}\parallel{/tex} CD. Find the value of x{tex}^\circ{/tex} in each case.

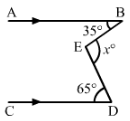
  37. The internal and external diameters of a hollow hemispherical vessel are 24 cm and 25 cm respectively. The cost of painting one sq. cm of the surface is 7 paise. Find the total cost to paint the vessel all over, (ignore the area of edge).
  38. The sides of a triangle are in the ratio 5:12:13, and its perimeter is 150 m. Find the area of the triangle.

    OR

    One side of a right triangle measures 126 m and the difference in lengths of its hypotenuse and other side is 42 cm. Find the measures of its two unknown sides and calculate its area. Verify the result using Heron’s Formula.

  39. Using factor theorem, factorize the polynomial: x4 + 10x3 + 35x2 + 50x + 24

  40. Section E Class 9 Maths Sample Paper 2023-24

  41. Read the text carefully and answer the questions:
    Reeta was studying in the class 9th C of St. Surya Public school, Mehrauli, New Delhi-110030
    Once Ranjeet and his daughter Reeta were returning after attending teachers’ parent meeting at Reeta’s school. As the home of Ranjeet was close to the school so they were coming by walking.
    Reeta asked her father, “Daddy how old are you?”
    Ranjeet said, “Sum of ages of both of us is 55 years, After 10 years my age will be double of you.

    1. What is the second equation formed?
    2. What is the present age of Reeta in years?
    3. What is the present age of Ranjeet in years?

    4. OR

      If the ratio of age of Reeta and her mother is 3 : 7 then what is the age of Reeta’s mother in years?

    To practice more questions & prepare well for exams, download myCBSEguide App. It provides complete study material for CBSE, NCERT, JEE (main), NEET-UG and NDA exams. Teachers can use Examin8 App to create similar papers with their own name and logo.

  42. Read the text carefully and answer the questions:
    Haresh and Deep were trying to prove a theorem. For this they did the following

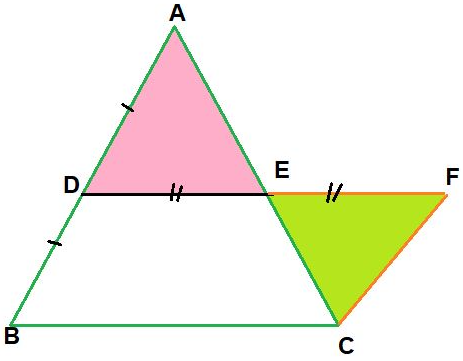
    1. Draw a triangle ABC
    2. D and E are found as the mid points of AB and AC
    3. DE was joined and DE was extended to F so DE = EF
    4. FC was joined.
    1. {tex}\triangle{/tex}ADE and {tex}\triangle{/tex}EFC are congruent by which criteria?
    2. Show that CF{tex}\parallel{/tex} AB.
    3. Show that CF = BD.

    4. OR

      Show that DF = BC and DF{tex}\parallel{/tex} BC.

  43. Read the text carefully and answer the questions:
    Rohan draws a circle of radius 10 cm with the help of a compass and scale. He also draws two chords, AB and CD in such a way that the perpendicular distance from the center to AB and CD are 6 cm and 8 cm respectively. Now, he has some doubts that are given below.

    1. Show that the perpendicular drawn from the Centre of a circle to a chord bisects the chord.
    2. What is the length of CD?
    3. What is the length of AB?

    4. OR

      How many circles can be drawn from given three noncollinear points?

Class 09  Mathematics Sample Paper Solution

  1. Section A Solution

  2. (d) 2 units
    Explanation: The distance from y-axis is equal to the x-coordinate, so distance = 2 units
  3. (c) 36 cm
    Explanation: {tex}36\sqrt 3 {/tex} = {tex}{{\sqrt 3 } \over 4}{/tex}a2
    a2  = {tex}{{36\sqrt 3 \times 4} \over {\sqrt 3 }}{/tex}= 144
    a = 12 cm
    Perimeter = {tex}3 \times 12{/tex} = 36 cm
  4. (d) {tex}{115^o}{/tex}
    Explanation:
    {tex}\angle APB=\angle BPQ=90^0{/tex}
    Now,
    In {tex}\triangle{/tex}APB,
    {tex}\angle{/tex}BAP + {tex}\angle{/tex}APB + {tex}\angle{/tex}ABP = 180o
    35o + 90o + {tex}\angle{/tex}ABP = 180o
    {tex}\angle{/tex}ABP = 55o
    Again,
    In {tex}\triangle{/tex}BPQ
    {tex}\Rightarrow{/tex} {tex}\angle{/tex}BPQ + {tex}\angle{/tex}PQB + {tex}\angle{/tex}PBQ = 180o
    {tex}\Rightarrow{/tex} 90o + 25o + {tex}\angle{/tex}PBQ = 180o
    {tex}\Rightarrow{/tex} {tex}\angle{/tex}PBQ = 65o
    Since, RBQ is a straight line,
    {tex}\angle{/tex}RBA + {tex}\angle{/tex}ABP + {tex}\angle{/tex}PBQ = 180o
    {tex}\angle{/tex}RBA + 55o + 65o = 180o
    {tex}\angle{/tex}RBA = 60o
    Finally,
    {tex}\angle{/tex}PBR = {tex}\angle{/tex}ABP + {tex}\angle{/tex}RBA
    = 55o + 60o = 115o
    To practice more questions & prepare well for exams, download myCBSEguide App. It provides complete study material for CBSE, NCERT, JEE (main), NEET-UG and NDA exams. Teachers can use Examin8 App to create similar papers with their own name and logo.
  5. (d) EC
    Explanation: By midpoint theorem of a triangle E is the midpoint of AC, hence AE = EC
  6. (d) -14
    Explanation: x = 2, y = -2
    x – yx-y = 2 – (-2)2-(-2)
    = 2 – (-2)2+2 
    = 2 – (-2)4
    = 2- (+16)
    = 2 – 16
    = -14
  7. (a) 50°
    Explanation: EC || AB and CD is transverse to it.
    Now {tex}\angle{/tex}ECD = {tex}\angle{/tex}AOD = 70° (Corresponding angles)
    In {tex}\angle{/tex}OBD
    {tex}\angle{/tex}OBD +  {tex}\angle{/tex}BOD + {tex}\angle{/tex}ODB = 180°
    {tex}\angle{/tex}BOD = 180° –  {tex}\angle{/tex}AOD = 180° – 70° = 110°
    {tex}\angle{/tex}ODB = 20° (Given)
    So {tex}\angle{/tex}OBD = 180° –  {tex}\angle{/tex}BOD – {tex}\angle{/tex}ODB
    = 180° – 110° – 20°
    = 50°
  8. (b) {tex}x = \frac{{3y + 5}}{2}{/tex}
    Explanation: {tex}\eqalign{ & 2x – 3y – 5 = 0 \cr & 2x = 3y + 5 \cr & x = {{3y + 5} \over 2} \cr}{/tex}
  9. (a) 23
    Explanation: Using ,(a + b)2 = a2 + b2 + 2ab
    {tex}\left(x+\frac{1}{x}\right)^{2}{/tex} = {tex}x^{2}+\left(\frac{1}{x^{2}}\right){/tex} + {tex}2 x \frac{1}{x}{/tex}
    {tex}\Rightarrow{/tex} (5)2 = x2 + {tex}\left(\frac{1}{x^{2}}\right){/tex} + 2
    {tex}\Rightarrow{/tex} {tex}x^{2}+\frac{1}{x^{2}}{/tex} = 25 – 2
    {tex}x^{2}+\frac{1}{x^{2}}{/tex} = 23
  10. (b) 1
    Explanation: {tex}\frac{3-\sqrt{5}}{3+2 \sqrt{5}}=a \sqrt{5}-\frac{19}{11} b{/tex}
    taking LHS,
    {tex}\Rightarrow \frac{3-\sqrt{5}}{3+2 \sqrt{5}} \times \frac{3-2 \sqrt{5}}{3-2 \sqrt{5}}{/tex}
    {tex}\Rightarrow \frac{3(3-2 \sqrt{5})-\sqrt{5}(3-2 \sqrt{5})}{9-20}{/tex}
    {tex}\Rightarrow \frac{9-6 \sqrt{5}-3 \sqrt{5}+10}{-11}{/tex}
    {tex}\Rightarrow \frac{19-9 \sqrt{5}}{-11}{/tex}
    {tex}\Rightarrow \frac{-19}{11}+\frac{9 \sqrt{5}}{11}{/tex}
    equating this with RHS,
    we get,
    {tex}\frac{-19}{11} b=-\frac{19}{11}{/tex}
    {tex}\Rightarrow{/tex} b = 1
  11. (c)  51 cm
    Explanation: {tex}\Rightarrow{/tex} ln {tex}\triangle A B C{/tex}, R and P are the mid-points of AB and BC
    {tex}\therefore R P \| A C,{/tex} {tex}R P=\frac{1}{2} A C{/tex} [By mid-point theorem] In a quadrilateral RPQA,
    {tex}\Rightarrow R P \| A Q{/tex}, RP = AQ
    {tex}\therefore{/tex} RPQA is a parallelogram
    {tex}\Rightarrow A R=\frac{1}{2} A B{/tex}
    {tex}\therefore A R=\frac{1}{2} \times 30=15 \mathrm{cm}{/tex}
    {tex}\Rightarrow{/tex} AR = PQ = 15cm [Since, opposite sides are equal] {tex}\Rightarrow R P=\frac{1}{2} A C=\frac{1}{2} \times 21=10.5 \mathrm{cm}{/tex} [Since, opposite sides are equal] {tex}\Rightarrow{/tex} Perimeter of ARPQ = AR + QP + RP + AQ
    = 15 + 15 + 10.5 + 10.5
    = 51cm
    {tex}\therefore{/tex} Perimeter of ARPQ is 51 cm
  12. (d) 3
    Explanation: 3 + 2x = {tex}(64)^{\frac{1}{2}}+ (27)^{\frac{1}{3}}{/tex}
    {tex}\Rightarrow{/tex} 3 + 2x = {tex}\sqrt {64} + \sqrt[3]{27}{/tex}
    {tex}\Rightarrow{/tex} 3 + 2x = 8 + 3
    {tex}\Rightarrow{/tex} 2x= 8 = 23
    equating both,
    x = 3
  13. (b) 1.x + 0.y = 7
    Explanation: The equation x = 7 in two variables can be written as exactly 1.x + 0.y = 7
    because it contain two variable x and y and coefficient of y is zero as there is no term containing y
    in equation x = 7
  14. (b) 30°, 60°
    Explanation: x + y + 90° = 180° (Linear Pair)
    2a + a + 90° = 180° (Since, x:y = 2:1)
    a =  30°
    x = 2a = {tex} \angle{/tex}COE = 60° (Vertically opposite angles)
    y = {tex} \angle{/tex}BOD = 30° (Vertically opposite angles)
  15. (d) {tex}\frac{\sqrt{5}-\sqrt{2}}{3}{/tex}
    Explanation: {tex}\frac{1}{\sqrt{5}+\sqrt{2}}{/tex}
    ={tex}\frac{\sqrt{5}-\sqrt{2}}{(\sqrt{5}+\sqrt{2})(\sqrt{5}-\sqrt{2})}{/tex}
    = {tex}\frac{\sqrt{5}-\sqrt{2}}{3}{/tex}
  16. (a) {tex}{50^o}{/tex}
    Explanation:
    Angle made at centre by an arc is double the angle made by it on any point on the circumference.
  17. (a) 4 units
    Explanation: Distance of point from y-axis is x -coordinate of given point,
    So, since, value of x-coordinate is 4
    so, distance = 4 units
  18. (a) y = 9x – 7
    Explanation: Since all the given co- ordinate (1, 2), (-1, -16) and (0, -7) satisfy the given line y = 9x – 7
    For point (1, 2)
    y = 9x – 7
    2 = 9(1) – 7
    2 = 9 – 7
    2 = 2
    Hence (2, 1) is a solution.
    For point (-1, -16)
    y = 9x – 7
    -16 = 9(-1) – 7
    -16 = -9 – 7
    -16 = -16
    Hence (-1, -16) is a solution.
    For point (0,-7)
    y = 9x – 7
    -7 = 9(0) -7
    -7 = -7
    Hence (0, -7) is a solution.
  19. (a) 3xyz
    Explanation: x3 + y3 + z3 – 3xyz = (x + y + z) (x2 + y2 + z2 – xy – yz – zx)
    =  x3 + y3 + z3 – 3xyz = (0) (x2 + y2 + z2 – xy – yz – zx)
    = x3 + y3 + z3 – 3xyz = 0
    = x3 + y3 + z3 – 3xyz
    If x + y + z = 0, then x3 + y3 + z3 is
    3xyz
  20. (a) Both A and R are true and R is the correct explanation of A.
    Explanation: Both A and R are true and R is the correct explanation of A.
  21. (d) A is false but R is true.
    Explanation: {tex}\sqrt{2}+\sqrt{3} \neq 5{/tex}
    {tex}\sqrt{3} + \sqrt{2}{/tex} = 1.732 + 1.414 = 3.146 {tex}\ne{/tex} {tex}\sqrt{5}{/tex} as {tex}\sqrt{5}{/tex} = 2.236

  22. Section B Sample Paper Solution

  23. We have AX = CY [Given] Now, by Euclid’s axiom 6, we have things which are double of the same thing are equal to one another,
    so 2AX = 2CY
    Hence, AC = BC. [{tex}\because{/tex} X and Y are the mid- points of AC and BC]
  24. From the given condition, we get the following figure

    In the above figure, PQ coincides with PR – QR.
    So, according to Euclid’s axiom, “things” which coincide with one another are equal to ‘one another’. We have,
    PQ + QR = PR i.e. PR – QR = PQ.
  25. (i) (+, +) are the signs of the co-ordinates of points in the I quadrant.
    ∴ A(1, 1) lies in the I quadrant.
    (ii) (–, –) are the signs of the co-ordinates of points in the III quadrant.
    ∴ B(–2, –4) lies in the III quadrant.
    (iii) (+, –) are the signs of the co-ordinates of points in the IV quadrant.
    ∴ C(1, –2) lies in the IV quadrant.
  26. {tex}\frac{1}{9}{/tex} = 0.111 … {tex}=0 . \overline{1}{/tex}

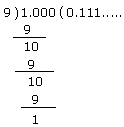
    OR

    {tex}\left(\frac{1}{3^{3}}\right)^{7}=\frac{1^{7}}{\left(3^{3}\right)^{7}}{/tex}{tex}=\frac{1}{3^{21}}=3^{-21}{/tex}

  27. Let the radii of bases, vertical heights and volumes of the two cones be r1, h1, v1 and r2, h2, v2 respectively.
    According to the question,
    {tex}{v_1\over v_2}={4\over5}{/tex} . . . .(1)
    {tex}{r_1\over r_2}={2\over3}{/tex} . . .(2)
    From (1), we have
    {tex}{{{1\over3}\pi r_1^2h_1}\over{{1\over3}\pi r_2^2h_2}}={4\over5}{/tex}
    {tex}\Rightarrow{/tex} {tex}{{r_1^2h_1}\over{r_2^2h_2}}={4\over5}{/tex}{tex}\Rightarrow{/tex} {tex}({r_1\over r_2})^2{h_1\over h_2}={4\over5}{/tex}
    {tex}\Rightarrow{/tex} {tex}({2\over3})^2{h_1\over h_2}={4\over5}{/tex}
    {tex}\Rightarrow{/tex} {tex}{h_1\over h_2}={4\over5}({3\over2})^2{/tex} . . . [Using (2)] {tex}\Rightarrow{/tex}{tex}{h_1\over h_2}={9\over5}{/tex}
    {tex}\therefore{/tex} The ratio of their vertical height is 9 : 5

    OR

    A cylinder and a cone have equal heights and equal radii of their bases.
    So, According to the question,
    = {tex}\frac{Curved \ surface \ area \ of \ cylinder}{Curved \ surface \ area \ of \ cone}{/tex} = {tex}\frac{2 \pi rh}{\pi rl}{/tex} = {tex}\frac{2 \pi rh}{\pi r \sqrt{r^{2}+h^{2}}}{/tex}
    {tex}\frac{8}{5}{/tex} = {tex}\frac{2 h}{\sqrt{r^{2}+h^{2}}}{/tex}
    {tex}\Rightarrow{/tex}{tex}\frac{64}{25}{/tex} = {tex}\frac{4h^2}{r^2 + h^2}{/tex}
    {tex}\Rightarrow{/tex} 64r2 + 64h2 = 100h2
    {tex}\Rightarrow{/tex} 64r2 = 100h2 – 64h2
    {tex}\Rightarrow{/tex} 64r2 = 36h2
    {tex}\Rightarrow{/tex} {tex}\frac{r^2}{h^2}{/tex} = {tex}\frac{36}{64}{/tex} = {tex}\frac{9}{16}{/tex}
    {tex}\Rightarrow{/tex}{tex}\frac{r}{h}{/tex} = {tex}\frac{3}{4}{/tex}
    {tex}\therefore{/tex} r:h = 3:4

  28. Section C Sample Paper Solution

  29. Given,
    {tex}\sqrt{2}{/tex}  = 1.4142
    Now, {tex}\sqrt{\frac{\sqrt{2}-1}{\sqrt{2}+1}}=\sqrt{\frac{(\sqrt{2}-1)}{(\sqrt{2}+1)} \times \frac{(\sqrt{2}-1)}{(\sqrt{2}-1)}}{/tex} [by rationalising] {tex}=\sqrt{\frac{(\sqrt{2}-1)^{2}}{2-1}}=\frac{\sqrt{(\sqrt{2}-1)^{2}}}{1}{/tex} [{tex}\because{/tex}(a + b)(a – b) = a2 – b2] {tex}=\sqrt{2}{/tex} – 1 = 1.4142 – 1 [{tex}\because \sqrt{2}{/tex} = 1.4142] = 0.4142
  30. In the given frequency distribution, the class intervals are not of equal width. {tex}\therefore{/tex} we would make modification in the lengths of the
    rectangle in the histogram so that the areas of the rectangle are proportional to the frequencies.

    MarksFrequencyWidth of the classLength of the rectangle
    {tex}10-20{/tex}{tex}6{/tex}{tex}10{/tex}{tex}\frac{10}{10} \times 6{/tex} {tex}= 6{/tex}
    {tex}20-30{/tex}{tex}17{/tex}{tex}10{/tex}{tex}\frac{10}{10} \times 17{/tex} {tex}= 17{/tex}
    {tex}30-50{/tex}{tex}15{/tex}{tex}20{/tex}{tex}\frac{10}{20} \times 15{/tex} {tex}= 7.5{/tex}
    {tex}50-70{/tex}{tex}16{/tex}{tex}20{/tex}{tex}\frac{10}{20} \times 16{/tex} {tex}= 8{/tex}
    {tex}70-100{/tex}{tex}26{/tex}{tex}30{/tex}{tex}\frac{10}{30} \times 26{/tex} {tex}= 8.67{/tex}

    The histogram of data is given below:

  31. In order to prove that BE is the median, it is sufficient to show that E is the mid-point of AC.
    Now, AD is the median in {tex}\triangle{/tex}ABC {tex}\Rightarrow{/tex} D is the mid-point of BC.
    Since DE is a line drawn through the mid-point of side BC of {tex}\triangle{/tex}ABC and is parallel to AB (given). Therefore, E is the mid-point of AC.
    Hence, BE is the median of {tex}\triangle{/tex}ABC.
  32. We have the equation as 3x + 2y = 18
    In standard form
    3x + 2y – 18 = 0
    Or 3x + 2y + (-18) =0
    But standard linear equation is
    ax + by + c = 0
    On comparison we get, a = 3, b = 2, c = -18
    If (4, 3) lie on the line, i.e., solution of the equation LHS = RHS
    {tex}\therefore{/tex} 3(4) + 2(3) = 18
    12 + 6 = 18
    18 = 18
    As LHS = RHS, Hence (4, 3) is the solution of given equation.
    Again for (1,2)
    3x + 2y = 18
    {tex}\therefore{/tex} 3(1)+2(2)=18
    3 + 4 = 18
    7 = 18
    LHS {tex}\neq{/tex} RHS
    Hence (1, 2) is not the solution of given equation.
    Therefore (4,3) is the point where the equation of the line 3x + 2y = 18 passes through where as the line for the equation 3x + 2y =18 does not pass through the point (1,2).
  33. The production of oil (in lakh tonnes) in some of the refineries in India during 1982

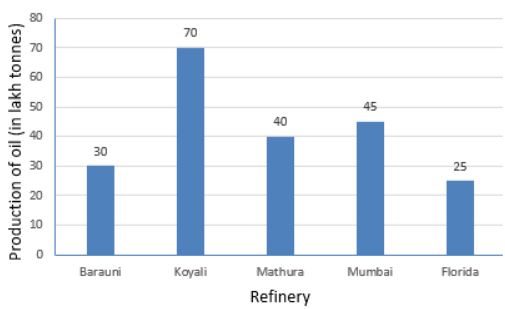
    OR

    The given table is in inclusive form. So, we first convert it into an exclusive form, as given below.

    Ages (in years)Number of teachers
    19.5 – 24.510
    24.5 – 29.528
    29.5 – 34.532
    34.5 – 39.548
    39.5 – 44.550
    44.5 – 49.535
    49.5 – 54.512

    A histogram for this table is shown in the figure given below:

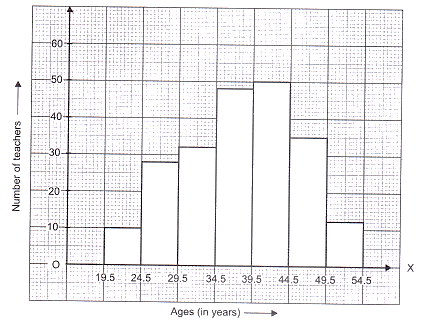
  34. We have,
    (x + y + z)2 + (x + {tex}\frac{y}{2}{/tex} + {tex}\frac{z}{3}{/tex})2 – ({tex}\frac{x}{2}{/tex} + {tex}\frac{y}{3}{/tex} + {tex}\frac{z}{4}{/tex})2
    = [x2 + y2 + z2 + 2(xy + yz + zx)] + [x2 + {tex}\frac{y^2}{4}{/tex} + {tex}\frac{z^2}{9}{/tex} + 2({tex}\frac{xy}{2}{/tex} + {tex}\frac{yz}{6}{/tex} + {tex}\frac{zx}{3}{/tex})] – [{tex}\frac{x^2}{4}{/tex} + {tex}\frac{y^2}{9}{/tex} + {tex}\frac{z^2}{16}{/tex} + 2({tex}\frac{xy}{6}{/tex} + {tex}\frac{yz}{12}{/tex} + {tex}\frac{zx}{8}{/tex})] = x2 + y2 + z2 + 2xy + 2yz + 2zx + x2 + {tex}\frac{y^{2}}{4}{/tex} + {tex}\frac{z^{2}}{9}{/tex} + {tex}\frac{2 x y}{2}{/tex} + {tex}\frac{2 y z}{6}{/tex} + {tex}\frac{2 z x}{3}{/tex} – {tex}\frac{x^{2}}{4}{/tex} – {tex}\frac{y^2}{9}{/tex} – {tex}\frac{z^{2}}{16}{/tex} – {tex}\frac{2 x y}{6}{/tex} – {tex}\frac{2 y z}{12}{/tex} – {tex}\frac{2 z x}{8}{/tex}
    = 2x2 – {tex}\frac{x^{2}}{4}{/tex} + y2 + {tex}\frac{y^{2}}{4}-\frac{y^{2}}{9}{/tex} + z2 + {tex}\frac{z^{2}}{9}-\frac{z^{2}}{16}{/tex} + 2xy + xy – {tex}\frac{x y}{3}{/tex} + 2yz + {tex}\frac{y z}{3}-\frac{y z}{6}{/tex} + 2zx + {tex}\frac{2 z x}{3}-\frac{z x}{4}{/tex}
    = {tex}\frac{8 x^{2}-x^{2}}{4}{/tex} + {tex}\frac{36 y^{2}+9 y^{2}-4 y^{2}}{36}{/tex} + {tex}\frac{144 z^{2}+16 z^{2}-9 z^{2}}{144}{/tex} + {tex}\frac{6 x y+3 x y-x y}{3}{/tex} + {tex}\frac{12 y z+2 y z-y z}{6}{/tex} + {tex}\frac{24 z x+8 z x-3 z x}{12}{/tex}
    = {tex}\frac{7 x^{2}}{4}{/tex} + {tex}\frac{41 y^{2}}{36}{/tex} + {tex}\frac{151 z^{2}}{144}{/tex} + {tex}\frac{8 x y}{3}{/tex} + {tex}\frac{13 y z}{6}{/tex} + {tex}\frac{29 z x}{12}{/tex}

  35. Section D Sample Paper Solution


  36. Given, CD {tex}\parallel{/tex} EF and EP is a transversal.
    {tex}\therefore{/tex} {tex}\angle{/tex}EPD + {tex}\angle{/tex}FEP = 180o [since, sum of interior angles on the same side of the transversal EP is 180o] {tex}\Rightarrow{/tex} y + 45o = 180o [{tex}\because{/tex} {tex}\angle{/tex}FEP = 45o, given] {tex}\Rightarrow{/tex} y = 180o – 45o {tex}\Rightarrow{/tex} y = 135o
    Also, given AB {tex}\parallel{/tex} CD and BP  is a transversal.
    So, x = y [corresponding angles axiom] {tex}\therefore{/tex} x = 135o
    Now, AB {tex}\parallel{/tex} CD and CD {tex}\parallel{/tex} EF
    {tex}\therefore{/tex} AB {tex}\parallel{/tex} EF
    Then, {tex}\angle{/tex}EAB + {tex}\angle{/tex}FEA = 180o
    [since, sum of interior angles on the same side of the transversal EA is 180o] {tex}\Rightarrow{/tex} 90o + z + 45o = 180o [{tex}\because{/tex} EA {tex}\perp{/tex} AB {tex}\Rightarrow{/tex} {tex}\angle{/tex}EAB = 90o] {tex}\Rightarrow{/tex} z + 135o = 180o
    {tex}\Rightarrow{/tex} z = 180o – 135o
    {tex}\Rightarrow{/tex} z = 45o
    Hence, x = 135o, y = 135o and z = 45o

    OR


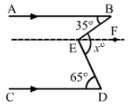
    Draw EF {tex}\parallel{/tex} AB {tex}\parallel{/tex} CD
    Now, AB {tex}\parallel{/tex} EF and BE is the transversal.
    Then,
    {tex}\angle A B E=\angle B E F{/tex} [Alternate Interior Angles] {tex}\Rightarrow \angle B E F=35^{\circ}{/tex}
    Again, EF {tex}\parallel{/tex} CD and DE is the transversal
    Then,
    {tex}\angle D E F=\angle F E D{/tex}
    {tex}\Rightarrow \angle F E D=65^{\circ}{/tex}
    {tex}\therefore x^{\circ}=\angle B E F+\angle F E D{/tex}
    x{tex}^\circ{/tex}= 35{tex}^\circ{/tex} + 65°
    x{tex}^\circ{/tex}= 100°

  37. Let R cm and r cm be respectively the external and internal radii of the hemispherical vessel. Then, R = 12.5 cm, r = 12 cm.
    Now,
    External surface area of the vessel = 2{tex}\pi R ^ { 2 }{/tex} = 2 {tex}\times \frac { 22 } { 7 } \times{/tex} (12.5)2 cm2
    Internal surface area of the vessel = 2{tex}\pi r ^ { 2 }{/tex} = 2 {tex}\times \frac { 22 } { 7 } \times{/tex} (12)2 cm2
    {tex}\therefore{/tex} Total area to be painted = 2 {tex}\times \frac { 22 } { 7 } \times{/tex} (12.5)2 + 2 {tex}\times \frac { 22 } { 7 } \times{/tex} 122 cm2
    {tex}\Rightarrow{/tex} Total area to be painted = 2 {tex}\times \frac { 22 } { 7 } \times{/tex} {({tex}\frac { 25 } { 2 }{/tex})2 + 122} cm2
    {tex}\Rightarrow{/tex} Total area to be painted = 2 {tex}\times \frac { 22 } { 7 } \times{/tex} ({tex}\frac { 625 } { 4 }{/tex} + 144) cm2 = {tex}\frac { 13211 } { 7 }{/tex} cm2
    Cost of painting at the rate of 7 paise per sq. cm = Rs. {tex}\frac { 13211 } { 7 } \times \frac { 7 } { 100 }{/tex} = Rs. 132.11
  38. According to question given sides are in the ratio of 5 : 12 : 13
    On dividing 150 m in the ratio 5 : 12 : 13, we get
    Length of one side ={tex}\left( 150 \times \frac { 5 } { 30 } \right) m = 25 m{/tex}
    Length of the second side = {tex}\left( 150 \times \frac { 12 } { 30 } \right) \mathrm { m } = 60 \mathrm { m }{/tex}
    Length of third side = {tex}\left( 150 \times \frac { 13 } { 30 } \right) m = 65 m{/tex}
    Let a = 25 m, b = 60 m, c = 65 m
    Then,    {tex}s = \frac { 1 } { 2 } ( 25 + 60 + 65 ) m = 75 m{/tex}
    Now (s – a) = 75 cm – 25 cm = 50 cm
    (s – b) = 75 cm – 60 cm = 15 cm
    (s – c) = 75 cm – 65 cm =  10 cm
    Area of the triangle = {tex}\sqrt { s( s – a ) ( s – b ) ( s – c ) }{/tex}
    {tex}= \sqrt { 75 \times 50 \times 15 \times 10 } \mathrm { m } ^ { 2 }{/tex}
    = 750 m2
    Hence, area of the triangle = 750 m2

    OR

    Let ABC be the right triangle right angles at C.

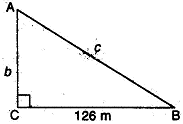
    a = 126 m . . . (1)
    In right triangle ACB.
    AB2 = AC2 + BC2 . . .[By Pythagoras theorem] {tex}\Rightarrow{/tex} c2 = a2 + b2
    {tex}\Rightarrow{/tex} c = {tex}\sqrt{a^2+b^2}{/tex} . . .(2)
    {tex}\Rightarrow{/tex} c – b = 42 . . .(3)
    {tex}\Rightarrow{/tex} {tex}\sqrt{a^2+b^2}{/tex}– b = 42 . . .[From (2)] {tex}\Rightarrow{/tex} {tex}\sqrt{126^2+b^2}{/tex} – b = 42 . . .[From (1)] {tex}\Rightarrow{/tex} {tex}\sqrt{126^2+b^2}{/tex} = (42+b)
    {tex}\Rightarrow{/tex} (126)2 + b2 = (42 + b)2
    {tex}\Rightarrow{/tex} 15876 + b2 = 1764 + b2 + 84b
    {tex}\Rightarrow{/tex} 84b = 15876 – 1764
    {tex}\Rightarrow{/tex} 84 b = 14112
    {tex}\Rightarrow{/tex} b =  {tex}\frac{14112}{84}{/tex}
    {tex}\Rightarrow{/tex} b = 168 m . . . (4)
    From (3) and (4)
    c – 168 = 42
    {tex}\therefore{/tex} c = 168 + 42 = 210 m . . . (5)
    {tex}\therefore{/tex} Area of the right triangle = {tex}\frac{1}{2}{/tex} {tex}\times{/tex} base {tex}\times{/tex} height
    ={tex}\frac{1}{2}{/tex}  {tex}\times{/tex} 126 {tex}\times{/tex} 168
    = 10584 m2
    Using Heron’s Formula
    a = 126 m, b = 168 m, c = 210 m
    {tex}\therefore{/tex}  s = {tex}\frac{a+b+c}{2}{/tex}
    = {tex}\frac{126+168+210}{2}{/tex} = {tex}\frac{504}{2}{/tex} = 252 m
    {tex}\therefore{/tex} Area of the right triangle
    = {tex}\sqrt{s(s-a)(s-b)(s-c)}{/tex}
    = {tex}\sqrt{252(252-126)(252-168)(252-210)}{/tex}
    = {tex}\sqrt{252(126)(84)(42)}{/tex}
    = {tex}\sqrt{(63 \times 4)(63 \times 2)(42 \times 2)(42)}{/tex}
    = 63 {tex}\times{/tex} 2 {tex}\times{/tex} 2 {tex}\times{/tex} 42 = 10584 m2

  39. Given, f(x) = x4 + 10x3 + 35x2 + 50x + 24
    The constant term in f(x) is equal to 24
    The factors of 24 are {tex}\pm{/tex}1, {tex}\pm{/tex}2, {tex}\pm{/tex}3, {tex}\pm{/tex}4, {tex}\pm{/tex}6, {tex}\pm{/tex}8, {tex}\pm{/tex}12, {tex}\pm{/tex}24
    Let, x + 1 = 0
    {tex}\Rightarrow{/tex} x = -1
    Substitute the value of x in f(x)
    f(-1) = (-1)4 + 10(-1)3 + 35(-1)2 + 50(-1) + 24
    = 1-10 + 35 – 50 + 24
    = 0
    {tex}\Rightarrow{/tex} (x + 1) is the factor of f(x)
    Similarly, (x + 2), (x + 3), (x + 4) are also the factors of f(x)
    Since, f(x) is a polynomial of degree 4, it cannot have more than four linear factors.
    {tex}\Rightarrow{/tex} f(x) = k(x + 1)(x + 2)(x + 3)(x + 4)
    {tex}\Rightarrow{/tex} x4 + 10x3 + 35x2 + 50x + 24 = k(x + 1)(x + 2)(x + 3)(x + 4)
    Substitute x = 0 on both sides
    {tex}\Rightarrow{/tex} 0 + 0 + 0 + 0 + 24 = k(1)(2)(3)(4)
    {tex}\Rightarrow{/tex} 24 = k(24)
    {tex}\Rightarrow{/tex} k = 1
    Substitute k = 1 in f(x) = k(x + 1)(x + 2)(x + 3)(x + 4)
    f(x) = (1)(x + 1)(x + 2)(x + 3)(x + 4)
    f(x) = (x + 1)(x + 2)(x + 3)(x + 4)
    hence, x4 + 10x3 + 35x2 + 50x + 24 = (x + 1)(x + 2)(x + 3)(x + 4)
    This is the required factorisation of f(x).

  40. Section E Sample Paper Solution

    1. x – 2y = 10
    2. x + y = 55 …(i) and x – 2y = 10 …(ii)
      Subtracting (ii) from (i)
      x + y – x + 2y = 55 – 10
      {tex}\Rightarrow{/tex} 3y = 45
      {tex}\Rightarrow{/tex} y = 15
      So present age of Reeta is 15 years.
    3. x + y = 55 …(i) and x – 2y = 10 …(ii)
      Subtracting (ii) from (i)
      x + y – x + 2y = 55 – 10
      {tex}\Rightarrow{/tex} 3y = 45
      {tex}\Rightarrow{/tex} y = 15
      Put y = 15 in equation (i)
      x + y = 55
      {tex}\Rightarrow{/tex} x + 15 = 55
      {tex}\Rightarrow{/tex} x = 55 − 15 = 40​​
      ​​​​​So Ranjeet’s present age is 40 years.

    4. OR

      Let Reeta;s mother age be ‘z’.
      Given Reeta age : Her mother age = 7 : 5
      We know that Reeta age = 15 years
      ​{tex}{Mother\,age\over Reeta\,age}={7\over 5}{/tex}
      {tex}\Rightarrow{/tex} z = {tex}\frac{7}{3} \times y{/tex}
      {tex}\Rightarrow{/tex} z = {tex} \frac{7}{3} \times 15{/tex}
      {tex}\Rightarrow{/tex} Here Mother age = 35 years
      Hence Reeta’s mother’s age is 35 years.

    To practice more questions & prepare well for exams, download myCBSEguide App. It provides complete study material for CBSE, NCERT, JEE (main), NEET-UG and NDA exams. Teachers can use Examin8 App to create similar papers with their own name and logo.

    1. {tex}\triangle{/tex}ADE and {tex}\triangle{/tex}CFE
      DE = EF (By construction)
      {tex}\angle{/tex}AED = {tex}\angle{/tex}CEF (Vertically opposite angles)
      AE = EC(By construction)
      By SAS criteria {tex}\triangle{/tex}ADE {tex}\cong{/tex}{tex}\triangle{/tex}CFE
    2. {tex}\triangle{/tex}ADE {tex}\cong{/tex} {tex}\triangle{/tex}CFE
      Corresponding part of congruent triangle are equal
      {tex}\angle{/tex}EFC = {tex}\angle{/tex}EDA
      alternate interior angles are equal
      {tex}\Rightarrow{/tex} AD ∥ FC
      {tex}\Rightarrow{/tex} CF ∥ AB
    3. {tex}\triangle{/tex}ADE {tex}\cong{/tex} {tex}\triangle{/tex}CFE
      Corresponding part of congruent triangle are equal.
      CF = AD
      We know that D is mid point AB
      {tex}\Rightarrow{/tex} AD = BD
      {tex}\Rightarrow{/tex} CF = BD

    4. OR

      DE = {tex}\frac{BC}{2}{/tex} {line drawn from mid points of 2 sides of {tex}\triangle{/tex} is parallel and half of third side}
      DE ∥ BC and DF ∥ BC
      DF = DE + EF
      {tex}\Rightarrow{/tex} DF = 2DE(BE = EF)
      {tex}\Rightarrow{/tex} DF = BC

    1. In {tex}\Delta{/tex}AOP and {tex}\Delta{/tex}BOP
      {tex}\angle{/tex}APO = {tex}\angle{/tex}BPO (Given)
      OP = OP (Common)
      AO = OB (radius of circle)
      {tex}\Delta{/tex}AOP {tex}\cong{/tex} {tex}\Delta{/tex}BOP
      AP = BP (CPCT)
    2. ​​​In right {tex}\Delta{/tex}COQ
      CO2 = OQ2 + CQ2
      {tex}\Rightarrow{/tex} 102 = 82 + CQ2
      {tex}\Rightarrow{/tex} CQ2 = 100 – 64 = 36
      {tex}\Rightarrow{/tex} CQ = 6
      CD = 2CQ
      {tex}\Rightarrow{/tex} CD = 12 cm​​
    3. In right {tex}\Delta{/tex}AOB
      AO2 = OP2 + AP2
      {tex}\Rightarrow{/tex} 102 = 62 + AP2
      {tex}\Rightarrow{/tex} AP2 = 100 – 36 = 64
      {tex}\Rightarrow{/tex} AP = 8
      AB = 2AP
      {tex}\Rightarrow{/tex} AB = 16 cm

    4. OR

      There is one and only one circle passing through three given non-collinear points.

 

Sample Papers for Class 9 all subjects 2023-24

To download sample papers for class 9 Science, Social Science, Mathematics, English Communicative, English language and literature, Hindi Course A, and Hindi Course B; do check myCBSEguide app or website. myCBSEguide provides sample papers with solutions, test papers for chapter-wise practice, NCERT solutions, NCERT Exemplar solutions, quick revision notes for ready reference, CBSE guess papers and CBSE important question papers. Sample papers all are made available through the best app for CBSE students and the myCBSEguide website.

myCBSEguide App

Test Generator

Create question paper PDF and online tests with your own name & logo in minutes.

Create Now
myCBSEguide App

myCBSEguide

Question Bank, Mock Tests, Exam Papers, NCERT Solutions, Sample Papers, Notes

Install Now

Related Posts

4 thoughts on “Class 9 Maths Sample Paper 2023-24”

Leave a Comment