
myCBSEguide App
Download the app to get CBSE Sample Papers 2023-24, NCERT Solutions (Revised), Most Important Questions, Previous Year Question Bank, Mock Tests, and Detailed Notes.
Install NowCBSE Class 12 Mathematics Vector Algebra Extra Questions. myCBSEguide has just released Chapter Wise Question Answers for class 12 Maths. There chapter wise Practice Questions with complete solutions are available for download in myCBSEguide website and mobile app. These Questions with solution are prepared by our team of expert teachers who are teaching grade in CBSE schools for years. There are around 4-5 set of solved Chapter 10 Vector Algebra Mathematics Extra Questions from each and every chapter. The students will not miss any concept in these Chapter wise question that are specially designed to tackle Board Exam. We have taken care of every single concept given in CBSE Class 12 Mathematics syllabus and questions are framed as per the latest marking scheme and blue print issued by CBSE for class 12.
Class 12 Chapter 10 Maths Extra Questions
Vector Algebra Extra Questions Class 12 Maths
Chapter 10 Vector Algebra
Find the angle between two vectors {tex}\vec a{/tex} and {tex}\vec b{/tex} with magnitudes {tex}\sqrt 3 {/tex} and 2, respectively, having {tex}\vec a\;.\vec b = \sqrt 6 {/tex}.
- {tex}\frac{\pi }{5}{/tex}
- {tex}\frac{\pi }{3}{/tex}
- {tex}\frac{\pi }{2}{/tex}
- {tex}\frac{\pi }{4}{/tex}
Find the angle between two vectors {tex}\hat i – 2\hat j + 3\hat k{/tex}and {tex}3\hat i – 2\hat j + \hat k\;{/tex}.
- {tex}{\cos ^{ – 1}}\left( {\frac{4}{7}} \right){/tex}
- {tex}{\cos ^{ – 1}}\left( {\frac{6}{7}} \right){/tex}
- {tex}{\cos ^{ – 1}}\left( {\frac{5}{9}} \right){/tex}
- {tex}{\cos ^{ – 1}}\left( {\frac{5}{7}} \right){/tex}
Vector has
- direction
- None of these
- magnitude
- magnitude as well as direction
Find the sum of the vectors{tex}\vec a = \hat i – 2\hat j + \hat k,\;\vec b = – 2\hat i + 4\hat j + 5\hat k\;{/tex} and {tex}\vec c = \hat i – 6\hat j – 7\hat k{/tex}.
- {tex} – \hat i + 4\hat j – \hat k{/tex}
- {tex} – 4\hat j – \hat k{/tex}
- {tex} – \hat i – 4\hat j – \hat k{/tex}
- {tex}\hat i – 4\hat j – \hat k{/tex}
Find the direction cosines of the vector {tex}\hat i + 2\hat j + 3\hat k{/tex}.
- {tex}\frac{1}{{\sqrt {14} }},\;\frac{2}{{\sqrt {14} }},\;\frac{3}{{\sqrt {14} }}{/tex}
- {tex}\frac{1}{{\sqrt {14} }},\;\frac{2}{{\sqrt {14} }},\; – \frac{3}{{\sqrt {14} }}{/tex}
- {tex}\frac{1}{{\sqrt {14} }},\; – \frac{2}{{\sqrt {14} }},\;\frac{3}{{\sqrt {14} }}{/tex}
- {tex} – \frac{1}{{\sqrt {14} }},\;\frac{2}{{\sqrt {14} }},\;\frac{3}{{\sqrt {14} }}{/tex}
- The values of k which {tex}|k \vec a | <|\vec a|{/tex} and {tex}k \vec a + \frac{1}{2}\vec a{/tex} is parallel to {tex}\vec a {/tex} holds true are ________.
- If {tex}\vec r. \vec a = 0{/tex}, {tex}\vec r. \vec b = 0{/tex}, and {tex}\vec r. \vec c = 0{/tex} for some non-zero vector {tex}\vec r{/tex}, then the value of {tex}\vec a (\vec b \times \vec c){/tex} is ________.
- The angle between two vectors {tex}\vec a{/tex} and {tex}\vec b{/tex} with magnitudes {tex}\sqrt 3{/tex} and 4, respectively, {tex}\vec a.\vec b{/tex} = {tex}2 \sqrt 3{/tex} is ________.
Find {tex}\vec a \times \vec b{/tex} if {tex}\vec a = 2\hat i + \hat j + 3\hat k,\vec b = 3\hat i + 5\hat j – 2\hat k{/tex}.
Find the projection of {tex}\vec { a } \text { on } \vec { b },{/tex} if {tex}\vec { a } \cdot \vec { b } = 8 {/tex} and {tex}\vec { b } = 2 \hat { i } + 6 \hat { j } + 3 \hat { k }.{/tex}
{tex}\vec a{/tex} Is unit vector and {tex}\left( {\vec x – \vec a} \right)\left( {\vec x + \vec a} \right) = 8{/tex}, Then find {tex}\left| {\vec x} \right|{/tex}.
Find the position vector of the mid-point of the vector joining the points P (2, 3, 4) and Q(4,1, – 2)
Find sine of the angle between the vectors. {tex}\vec a = 2\hat i – \hat j + 3\hat k,\vec b = \hat i + 3\hat j + 2\hat k{/tex}.
Find the projection of the vector {tex}\hat i + 3\hat j + 7\hat k{/tex} on the vector {tex}7\hat i – \hat j + 8\hat k{/tex}
Let {tex} \vec { a } = \hat { i } + \hat { j } + \hat { k } , \vec { b } = 4 \hat { i } – 2 \hat { j } + 3 \hat { k }{/tex} and {tex} \vec { c } = \hat { i } – 2 \hat { j } + \hat { k }.{/tex}Find a vector of magnitude 6 units, which is parallel to the vector {tex} 2 \vec { a } – \vec { b } + 3 \vec { c }.{/tex}
Let {tex}\vec a = \hat i + 4\hat j + 2\hat k,\vec b = 3\hat i – 2\hat j + 7\hat k{/tex} and {tex}\vec c = 2\hat i – \hat j + 4\hat k{/tex} .Find a vector {tex}\vec d{/tex} which is perpendicular to both {tex}\vec a{/tex} and {tex}\vec b{/tex} and {tex}\vec c.\vec d = 15{/tex}.
A girl walks 4 km towards west, then she walks 3 km in a direction {tex}{30^0}{/tex} east of north and stops. Determine the girl’s displacement from her initial point of departure.
Find a vector {tex}\vec d{/tex} which is {tex} \bot {/tex} to both {tex}\vec a{/tex} and {tex}\vec b{/tex} and {tex}\vec c{/tex}. {tex}\vec d = 15{/tex} Let {tex}\vec a = \hat i + 4\hat j + 2\hat k,\vec b = 3\hat i – 2\hat j + 7\hat k{/tex} and {tex}\vec c = 2\hat i – \hat j + 4\hat k{/tex}.
Chapter 10 Vector Algebra
Solution
- {tex}\frac{\pi }{4}{/tex}, Explanation: {tex}| {\overrightarrow a } | = \sqrt 3 ,| {\overrightarrow b } | = 2,\overrightarrow a .\overrightarrow b = \sqrt 6{/tex}
{tex}\Rightarrow \overrightarrow a .\overrightarrow b = | {\overrightarrow a } |.| {\overrightarrow b } |\cos \theta \Rightarrow \sqrt 6{/tex}
{tex} = 2\sqrt 3 \cos \theta{/tex}
{tex}\Rightarrow \cos \theta = \frac{1}{{\sqrt 2 }} \Rightarrow \theta = \frac{\pi }{4} {/tex}
- {tex}{\cos ^{ – 1}}\left( {\frac{5}{7}} \right){/tex}, Explanation: {tex}\overrightarrow a = \widehat i – 2\widehat j + 3\widehat k,\overrightarrow b = 3\widehat i – 2\widehat j + \widehat k {/tex}{tex}\Rightarrow | {\overrightarrow a } | = \sqrt {14} , | {\overrightarrow b } | = \sqrt {14}, \overrightarrow a .\overrightarrow b = 10{/tex}
{tex} \Rightarrow \frac{{\overrightarrow a .\overrightarrow b }}{{| {\overrightarrow a } || {\overrightarrow b } |}} = \cos \theta \Rightarrow \frac{{10}}{{14}} = \cos \theta {/tex}
{tex}\Rightarrow \cos \theta = \frac{5}{7} \Rightarrow \theta = {\cos ^{ – 1}}\frac{5}{7} \\\\\\ {/tex}
- magnitude as well as direction, Explanation: A vector has both magnitude as well as direction.
- {tex} – 4\hat j – \hat k{/tex}, Explanation: We have: vectors {tex}\vec{a}=\hat{i}-2\hat{j}+\hat{k},{/tex} {tex}\vec{b}=-2\hat{i}+4\hat{j}+5\hat{k}{/tex} and
- {tex}\frac{1}{{\sqrt {14} }},\;\frac{2}{{\sqrt {14} }},\;\frac{3}{{\sqrt {14} }}{/tex}, Explanation: Let {tex}\overrightarrow a =\hat i + 2\hat j + 3\hat k{/tex},Then, {tex}\widehat a = \frac{{\overrightarrow a }}{{\left| {\overrightarrow a } \right|}} = \frac{{\widehat i + 2\widehat j + 3\widehat k}}{{\sqrt {{1^2} + {2^2} + {3^2}} }} = \frac{{\widehat i + 2\widehat j + 3\widehat k}}{{\sqrt {14} }}{/tex}
Therefore , the D.C.’s of vector a are :
{tex}\frac{1}{{\sqrt {14} }},\;\frac{2}{{\sqrt {14} }},\;\frac{3}{{\sqrt {14} }}.{/tex}
- {tex}\frac{\pi }{4}{/tex}, Explanation: {tex}| {\overrightarrow a } | = \sqrt 3 ,| {\overrightarrow b } | = 2,\overrightarrow a .\overrightarrow b = \sqrt 6{/tex}
- k {tex}\in{/tex} ]-1, 1 [k {tex}\ne{/tex} {tex}-\frac{1}{2}{/tex}
- 0
- {tex}\frac{\pi}{3}{/tex}
- {tex}\vec a \times \vec b = \left| {\begin{array}{*{20}{c}} {\hat i}&{\hat j}&{\hat k} \\ 2&1&3 \\ 3&5&{ – 2} \end{array}} \right|{/tex}
{tex}= \hat i\left( { – 2 – 15} \right) – \hat j\left( { – 4 – 9} \right) + \hat k\left( {10 – 3} \right){/tex}
{tex} = – 17\hat i + 13\hat j + 7\hat k{/tex} - We are given that, {tex}\vec { a } \cdot \vec { b } = 8{/tex} and {tex}\vec { b } = 2 \hat { i } + 6 \hat { j } + 3 \hat { k }{/tex}
{tex}\therefore{/tex} The projection of {tex} \vec { a }{/tex} on {tex} \vec { b }{/tex} is given as = {tex}\frac { \vec { a } \cdot \vec { b } } { | \vec { b } | }{/tex}
{tex}= \frac { 8 } { \sqrt { 2 ^ { 2 } + 6 ^ { 2 } + 3 ^ { 2 } } }{/tex}
{tex}= \frac { 8 } { \sqrt { 4 + 36 + 9 } }{/tex}
{tex}= \frac { 8 } { \sqrt { 49 } } = \frac { 8 } { 7 }{/tex} - {tex}\left| {\vec a} \right| = 1{/tex}
{tex}\left( {\vec x – \vec a} \right).\left( {\vec x + \vec a} \right) = 8{/tex}
{tex}{\left| {\vec x} \right|^2} -| \vec a|^2= 8{/tex}
{tex}{\left| {\vec x} \right|^2} -1= 8{/tex}
{tex}{\left| {\vec x} \right|^2} = 9{/tex}
{tex}\left| {\vec x} \right| = 3{/tex} - Given: Point P (2, 3, 4) and Q(4,1, – 2)
{tex}\therefore{/tex} Position vector of point P is {tex}\vec a = 2\hat i + 3\hat j + 4\hat k{/tex}
And Position vector of point Q is {tex}\vec b = 4\hat i + \hat j – 2\hat k{/tex}
And Position vector of mid-point R of PQ is {tex}\frac{{\vec a + \vec b}}{2} = \frac{{2\hat i + 3\hat j + 4\hat k + 4\hat i + \hat j – 2\hat k}}{2}{/tex}
{tex}=\frac{{6\hat i + 4\hat j + 2\hat k}}{2} = 3\hat i + 2\hat j + \hat k{/tex} - {tex}\vec a \times \vec b = \left| {\begin{array}{*{20}{c}} {\hat i}&{\hat j}&{\hat k} \\ 2&{ – 1}&3 \\ 1&3&2 \end{array}} \right|{/tex}
{tex}= – 11\hat i – \hat j + 7\hat k{/tex}
{tex}\left| {\vec a \times \vec b} \right| = \sqrt {{{\left( { – 11} \right)}^2} + {{\left( { – 1} \right)}^2} + {{\left( 7 \right)}^2}} {/tex}
{tex} = \sqrt {171} = 3\sqrt {19} {/tex}
{tex}\sin \theta = \frac{{\left| {\vec a \times \vec b} \right|}}{{\left| {\vec a} \right|\left| {\vec b} \right|}} = \frac{{3\sqrt {19} }}{{\sqrt {14} .\sqrt {14} }} = \frac{3}{{14}}\sqrt {19}{/tex} - Let {tex}\vec a = \hat i + 3\hat j + 7\hat k{/tex} and {tex}\vec b = 7\hat i – \hat j + 8\hat k{/tex}
Projection of vector {tex}\vec a{/tex} on {tex}\vec b = \frac{{\vec a.\vec b}}{{\left| {\vec b} \right|}}{/tex}
{tex}= \frac{{\left( 1 \right)\left( 7 \right) + \left( 3 \right)\left( { – 1} \right) + 7\left( 8 \right)}}{{\sqrt {{{\left( 7 \right)}^2} + {{\left( { – 1} \right)}^2} + {{\left( 8 \right)}^2}} }}{/tex}
{tex}= \frac{{7 – 3 + 56}}{{\sqrt {49 + 61 + 64} }} = \frac{{60}}{{\sqrt {114} }}{/tex} - According to the question ,
{tex}\vec { a } = \hat { i } + \hat {j} + \hat { k } , {/tex}
{tex}\vec { b } = 4 \hat { i } – 2 \hat { j } + 3 \hat { k }{/tex} and
{tex} \vec { c } = \hat { i } – 2 \hat { j } + \hat { k }{/tex}
Now {tex},2 \vec { a } – \vec { b } + \vec { 3 } \vec { c }{/tex}
{tex} = 2 ( \hat { i } + \hat { j } + \hat { k } ) – ( 4 \hat { i } – 2 \hat { j } + 3 \hat { k } ) + 3 ( \hat { i } – 2 \hat { j}+ \hat { k } ){/tex}
{tex} = 2 \hat { i } + 2 \hat { j } + 2 \hat { k } – 4 \hat { i } + 2 \hat { j } – 3 \hat { k } + 3 \hat { i } – 6 \hat { j } + 3{ \hat { k } }{/tex}
{tex} = \hat { i } – 2 \hat {j } + { 2 } \hat { k }{/tex}
{tex} \Rightarrow \quad 2 \vec { a } – \vec { b } + 3 \vec { c } = \hat { i } – 2 \hat { j } + { 2 } \hat { k }{/tex}
Now, a unit vector in the direction of vector is {tex} 2 \vec { a } – \vec { b } + 3 \vec { c } = \frac { 2 \vec { a } – \vec { b } + 3 \vec { c } } { | 2 \vec { a } – \vec { b } + 3 \vec { c } | }{/tex}
{tex} = \frac { \hat { i } – 2 \hat { j } + 2 \hat { k } } { \sqrt { ( 1) ^ { 2 } + ( – 2 ) ^ { 2 } + ( 2 ) ^ { 2 } } }{/tex}
{tex} = \frac { \hat { i } – 2 \hat { j } + 2 \hat { k } } { \sqrt { 9 } }{/tex}
{tex}= \frac { \hat { i } – 2 \hat { j } + 2 \hat { k } } { 3 }{/tex}
{tex} = \frac { 1 } { 3 } \hat { i } – \frac { 2 } { 3 } \hat { j } + \frac { 2 } { 3 } \hat { k }{/tex}
Vector of magnitude 6 units parallel to the vector is ,
{tex} = 6 \left( \frac { 1 } { 3 } \hat { i } – \frac { 2 } { 3 } \hat { j } + \frac { 2 } { 3 } \hat { k } \right){/tex}
{tex} = 2 \hat { i } – 4 \hat { j } + 4 \hat { k }{/tex} - Given: Vectors {tex}\vec a = \hat i + 4\hat j + 2\hat k{/tex} and {tex}\vec b = 3\hat i – 2\hat j + 7\hat k{/tex}
We know that the cross-product of two vectors, {tex}\vec a \times \vec b{/tex} is a vector perpendicular to both {tex}\vec a{/tex} and {tex}\vec b{/tex}
Hence, vector {tex}\vec d{/tex} which is also perpendicular to both {tex}\vec a{/tex} and {tex}\vec b{/tex} is {tex}\vec d = \lambda \left( {\vec a \times \vec b} \right){/tex} where {tex}\lambda = 1{/tex} or some other scalar.
Therefore, {tex}\vec d = \lambda \left| {\begin{array}{*{20}{c}} \vec i&\vec j&\vec k \\ 1&4&2 \\ 3&{ – 2}&7 \end{array}} \right|{/tex}
{tex}= \lambda \left[ {\hat i\left( {28 + 4} \right) – \hat j\left( {7 – 6} \right) + \hat k\left( { – 2 – 12} \right)} \right]{/tex}
{tex} \Rightarrow \vec d = 32\lambda \hat i – \lambda \hat j – 14\lambda \hat k{/tex}…(i)
Now given {tex}\vec c = 2\hat i – \hat j + 4\hat k{/tex} and {tex}\vec c.\vec d = 15{/tex}
{tex}\vec c.\vec d = 15{/tex}
{tex}= 2\left( {32\lambda } \right) + \left( { – 1} \right)\left( { – \lambda } \right) + 4\left( { – 14\lambda } \right) = 15{/tex}
{tex} \Rightarrow 64\lambda + \lambda – 56\lambda = 15{/tex}
{tex} \Rightarrow 9\lambda = 15{/tex}
{tex} \Rightarrow \lambda = \frac{{15}}{9}{/tex}
{tex} \Rightarrow \lambda = \frac{5}{3}{/tex}
Putting {tex}\lambda = \frac{5}{3}{/tex} in eq. (i), we get
{tex}\vec d = \frac{5}{3}\left[ {32\hat i – \hat j – 14\hat k} \right]{/tex}
{tex}\Rightarrow \vec d = \frac{1}{3}\left[ {160\hat i – 5\hat j – 70\hat k} \right]{/tex} - Let the initial point of departure is origin (0, 0) and the girl walks a distance OA = 4 km towards west.
Through the point A, draw a line AQ parallel to a line OP, which is {tex}{30^0}{/tex} East of North, i.e., in East-North quadrant making an angle of {tex}{30^0}{/tex} with North.
Again, let the girl walks a distance AB = 3 km along this direction {tex}\overrightarrow {OQ} {/tex}
{tex}\therefore \overrightarrow {OA} = 4\left( { – \vec i} \right) = – 4\hat i{/tex} …(i) [{tex}\because {/tex} Vector {tex}\overrightarrow {OA} {/tex} is along OX’]
Now, draw BM perpendicular to x – axis.
In {tex}\Delta AMB{/tex} by Triangle Law of Addition of vectors,
{tex}\overrightarrow {AB} = \overrightarrow {AM} + \overrightarrow {MB} = \left( {AM} \right)\hat i + \left( {MB} \right)\hat i{/tex}
Dividing and multiplying by AB in R.H.S.,
{tex}\overrightarrow {AB} = AB\frac{{AM}}{{AB}}\hat i + AB\frac{{MB}}{{AB}}\hat j {/tex} {tex}= 3\cos {60^o}\hat i + 3\sin {60^o}\hat j{/tex}
{tex}\Rightarrow AB = 3\frac{1}{2}\hat i + 3\frac{{\sqrt 3 }}{2}\hat i = \frac{3}{2}\hat i + \frac{{3\sqrt 3 }}{2}j{/tex} …(ii)
{tex}\therefore{/tex} Girl’s displacement from her initial point O of departure to final point B,
{tex}\overrightarrow {OB} = \overrightarrow {OA} + \overrightarrow {AB} {/tex} {tex}= – 4\hat i + \left( {\frac{3}{2}\hat i + \frac{{3\sqrt 2 }}{2}\hat j} \right) {/tex} {tex}= \left( { – 4 + \frac{3}{2}} \right)\hat i + \frac{{3\sqrt 3 }}{2}\hat j{/tex}
{tex}\Rightarrow \overrightarrow {OB} = \frac{{ – 5}}{2}\hat i + \frac{{3\sqrt 3 }}{2}\hat j{/tex} - {tex}\vec a = \hat i + 4\hat j + 2\hat k,\vec b = 3\hat i – 2\hat j + 7\hat k{/tex} and {tex}\vec c = 2\hat i – \hat j + 4\hat k{/tex}
Let {tex}\vec d = x\hat i + y\hat j + z\hat k{/tex}
ATQ, {tex}\vec d.\vec a = 0,\vec d.\vec b = 0{/tex} and {tex}\vec c.\vec d = 15{/tex}, then,
x + 4y + 2z = 0 …(1)
3x – 2y + 7z = 0 …(2)
2x – y + 4z = 15 …(3)
On solving equation (1) and (2)
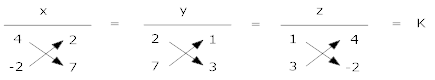
{tex}\frac{x}{{28 + 4}} = \frac{y}{{6 – 7}} = \frac{z}{{ – 2 – 12}} = k{/tex}
x = 32k, y = -k, z = -14k
Put x, y, z in equation (3)
2(32k) – (-k) + 4(-14k) = 15
64k + k – 56k = 15
9k = 15
{tex}k = \frac{{15}}{9}{/tex}
{tex}k = \frac{5}{3}{/tex}
{tex}x = 32 \times \frac{5}{3} = \frac{{160}}{3}{/tex}
{tex}y = – \frac{5}{3} {/tex}
{tex}z = – 14 \times \frac{5}{3} = – \frac{{70}}{3}{/tex}
{tex}\vec d = \frac{{160}}{3}\hat i – \frac{5}{3}\hat j – \frac{{70}}{3}\hat k{/tex}
Chapter Wise Important Questions Class 12 Maths Part I and Part II
- Relations and Functions
- Inverse Trigonometric Functions
- Matrices
- Determinants
- Continuity and Differentiability
- Application of Derivatives
- Integrals
- Application of Integrals
- Differential Equations
- Vector Algebra
- Three Dimensional Geometry
- Linear Programming
- Probability

Test Generator
Create question paper PDF and online tests with your own name & logo in minutes.
Create Now
myCBSEguide
Question Bank, Mock Tests, Exam Papers, NCERT Solutions, Sample Papers, Notes
Install Now