CBSE Sample Papers Class 11 Physics 2024

myCBSEguide App

Download the app to get CBSE Sample Papers 2023-24, NCERT Solutions (Revised), Most Important Questions, Previous Year Question Bank, Mock Tests, and Detailed Notes.

Install Now

CBSE Sample Papers Class 11 Physics 2023-24

CBSE Sample Papers Class 11 Physics myCBSEguide provides CBSE Class 11 Sample Papers of Physics for the year 2023-24 with solutions in PDF format for free download. The CBSE Sample Papers for all – NCERT books and based on CBSE latest syllabus must be downloaded and practiced by students. Class 11 Physics New Sample Papers follow the blueprint of that year only. A student must check the latest syllabus and marking scheme. Sample papers for Class 11 Physics and other subjects are available for download as PDF in-app too. myCBSEguide provides sample papers with solutions for the year 2024.

Download Physics Sample Papers as PDF

Class 11 – Physics Sample Paper (2023-24)

Maximum Marks: 70
Time Allowed: : 3 hours

General Instructions:

1. There are 33 questions in all. All questions are compulsory.
2. This question paper has five sections: Section A, Section B, Section C, Section D and Section E. All the sections are compulsory.
3. Section A contains sixteen questions, twelve MCQ and four Assertion Reasoning based of 1 mark each, Section B contains five questions of two marks each, Section C contains seven questions of three marks each, Section D contains two case study-based questions of four marks each and Section E contains three long answer questions of five marks each.
4. There is no overall choice. However, an internal choice has been provided in section B, C, D and E. You have to attempt only one of the choices in such questions.
5. Use of calculators is not allowed.

1. Physics Sample Paper Section A

2. Young’s modulus of steel is 1.9 {tex}\times{/tex} 10¹¹ N/m². When expressed in CGS units of dynes/cm², it will be equal to (1N = 10⁵ dyne, 1m² = 10⁴ cm²)
   a) 1.9 {tex}\times{/tex} 10¹⁰
   b) 1.9 {tex}\times{/tex} 10¹¹
   c) 1.9 {tex}\times{/tex} 10¹²
   d) 1.9 {tex}\times{/tex} 10¹³
3. The human ear is most sensitive to sound in the frequency range of:
   a) 1000 to 2000 Hz
   b) 200 to 400 Hz
   c) 10000 to 20000 Hz
   d) 20 to 20000 Hz
4. Centre of gravity can be defined:
   a) as that point where the total gravitational torque on the body is greater than zero
   b) as the center of mass
   c) as that point where the total gravitational torque on the body is zero
   d) as that point where the total gravitational force on the body is zero
5. What will be the height of a liquid column in a capillary tube on the surface of the moon?
   a) 1/6th of what was on earth’s surface
   b) Six times that on the earth’s surface
   c) It will remain unchanged
   d) 36 times that on earth’s surface
6. The formula for gravitational potential energy associated with two particles of masses m₁ and m₂ separated by distance r is given by
   a) {tex}{\rm{v}} = – \frac{G{m_1}}{r}{/tex}
   b) {tex}{\rm{v}} = – \frac{G{m_1}{m_2}}{r}{/tex}
   c) {tex}\mathrm{v}=-\frac{G m_2}{r}{/tex}
   d) {tex}\mathrm{v}=-\frac{G m_1 m_2}{2 r}{/tex}

   To practice more questions & prepare well for exams, download myCBSEguide App. It provides complete study material for CBSE, NCERT, JEE (main), NEET-UG and NDA exams. Teachers can use Examin8 App to create similar papers with their own name and logo.

7. A source of sound gives 5 beats per second when sounded with another source of frequency 100 second^-1. The second harmonic of the source, together with a source of frequency 205 sec^-1 gives 5 beats per second. What is the frequency of the source?
   a) 100 second^-1
   b) 105 second ^-1
   c) 205 second^-1
   d) 95 second^-1
8. Motion along a straight line is called __________.
   a) parabolic motion
   b) circular motion
   c) oscillatory motion
   d) rectilinear motion
9. A transverse wave is represented by y = sin ({tex}\omega{/tex}t – kx) For what value of the wavelength is the wave velocity equal to the maximum particle velocity?
   a) {tex}\frac{\pi A}{2}{/tex}
   b) {tex}\pi A{/tex}
   c) 2 {tex}\pi{/tex}A
   d) A
10. Pressures inside two soap bubbles are 1.01 atm and 1.03 atm, ratio between their volumes is
    a) 3 : 1
    b) none of these
    c) 27 : 1
    d) 127 : 101
11. There is no atmosphere on the moon, because
    1. it is closer to the earth and also it has the inactive inert gases in it.
    2. it is too far from the sun and has very low pressure in its outer surface.
    3. escape velocity of gas molecules is greater than their root mean square velocity.
    4. escape velocity of gas molecules is less than their root mean square velocity.
    a) Option ii
    b) Option i
    c) Option iii
    d) Option iv
12. Two rings of radii R and nR made from the same wire have the ratio of moments of inertia about an axis passing through their centre equal to 1 : 8. The value of n is
    a) 2
    b) 4
    c) {tex}2 \sqrt{2}{/tex}
    d) {tex}\frac{1}{2}{/tex}
13. When water is heated from 0°C to 10°C its volume
    a) increases continuously
    b) first decreases and then increases
    c) decreases continuously
    d) first increases and then decreases
14. Assertion: n small balls each of mass m colliding plastically each second on surface which velocity u. The force experienced by the surface is 2mnu.
    Reason: On elastic collision, the ball rebounds with the same velocity.
    a) Assertion and reason both are correct statements and reason is correct explanation for assertion.
    b) Assertion and reason both are correct statements but reason is not correct explanation for assertion.
    c) Assertion is correct statement but reason is wrong statement.
    d) Assertion is wrong statement but reason is correct statement.
15. Assertion: The value of AQ is always zero in adiabatic process.
    Reason: Adiabatic process is always a cyclic process.
    a) Assertion and reason both are correct statements and reason is correct explanation for assertion.
    b) Assertion and reason both are correct statements but reason is not correct explanation for assertion.
    c) Assertion is correct statement but reason is wrong statement.
    d) Assertion is wrong statement but reason is correct statement.
16. Assertion (A): If earth were a hollow sphere, gravitational field intensity at any point inside the earth would be zero.
    Reason (R): Net force on a body inside the sphere is zero.
    a) Both A and R are true and R is the correct explanation of A.
    b) Both A and R are true but R is not the correct explanation of A.
    c) A is true but R is false.
    d) A is false but R is true.
17. Assertion (A): In projectile motion, the angle between the instantaneous velocity and acceleration at the highest point is 180°.
    Reason (R): At the highest point, velocity of projectile will be in horizontal direction only.
    a) Both A and R are true and R is the correct explanation of A.
    b) Both A and R are true but R is not the correct explanation of A.
    c) A is true but R is false.
    d) A is false but R is true.

18. Physics Sample Paper Section B

19. At what temperature (in °C) will the speed of sound in air be 3 times its value at 0°C?
20. In the relation p = {tex}( a / b ) e ^ { – ( a z / \theta )}{/tex}, p is the pressure, z is the distance, and {tex}\theta{/tex} is the temperature. What is the dimensional formula of b?
21. A gas bubble, from an explosion underwater, oscillates with a period T proportional to p^a d^b E^c, where p is the static pressure, d is the density of water and E is the total energy of the explosion. Find the values of a, b and c.
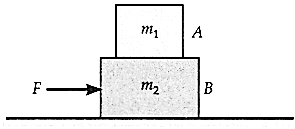
22. A block A of mass 4 kg is placed on another block B of mass 5 kg, and the block B rests on a smooth horizontal table. For sliding the block A on B, a horizontal force of 12 N is required to be applied on it. How much maximum horizontal force can be applied on B so that both A and B move together? Also find out the acceleration produced by this force.
    
23. The distance of the planet Jupiter from the sun is 5.2 times that of the earth. Find the period of the Jupiter’s revolution around the sun?

    OR

    What is the difference between inertial mass and gravitational mass of a body?

24. Physics Sample Paper Section C

25. Eight rain drops of radius 1 mm each falling down with terminal velocity of 5 cms^-1 coalesce to form a bigger drop. Find the terminal velocity of the bigger drop.
26. Develop a relation between the co-efficient of linear expansion, co-efficient superficial expansion and coefficient of cubical expansion of a solid.
27. A parachutist bails out from an aeroplane and after dropping through a distance of 40 m, he opens the parachute and decelerates at 2 ms^-2. If he reaches the ground with a speed of 2 ms^-1, how long is he in the air? At what height did he bailout from the plane?
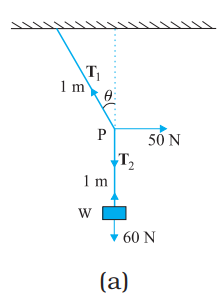
28. A mass of 6 kg is suspended by a rope of length 2 m from the ceiling. A force of 50 N in the horizontal direction is applied at the midpoint P of the rope, as shown. What is the angle the rope makes with the vertical in equilibrium? (Take g = 10 ms^-2). Neglect the mass of the rope.
    
29. Explain, why?
    1. 500 J of work is done on a gas to reduce its volume by compression adiabatically. What is the change in internal energy of the gas?
    2. The coolant in a chemical or a nuclear plant, i.e. the liquid used to prevent the different parts of a plant from getting too hot should have high specific heat.
    3. The climate of a harbour town is more temperate than that of a town in a desert at the same latitude.
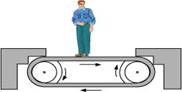
30. Figure shows a man standing stationary with respect to a horizontal conveyor belt that is accelerating with 1 ms^-2. What is the net force on the man? If the coefficient of static friction between the man’s shoes and the belt is 0.2, up to what acceleration of the belt can the man continue to be stationary relative to the belt? (Mass of the man = 65 kg.)
    
31. Briefly discuss how Pascal’s law is affected by gravity. Hence obtain Pascal’s law of transmission of pressure.

    OR

    To what height should a cylindrical vessel be filled with a homogeneous liquid to make the force, with which the liquid presses the side of the vessel equal to the force exerted by the liquid on the bottom of the vessel?

32. Physics Sample Paper Section D

33. Read the text carefully and answer the questions:
    Elastic potential energy is Potential energy stored as a result of the deformation of an elastic object, such as the stretching of a spring. It is equal to the work done to stretch the spring, which depends upon the spring constant k as well as the distance stretched
    
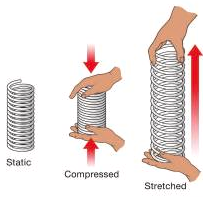
    1. If stretch in spring of force constant k is doubled, then the ratio of final to initial forces is:
       a) 4:1
       b) 1:4
       c) 2:1
       d) 1:2
    2. A light body and a heavy body have the same kinetic energy. which one has greater linear momentum?
       a) light body
       b) both heavy and light body
       c) none of these
       d) heavy body
    3. A spring is cut into two equal halves. How is the spring constant of each half affected?
       a) becomes double
       b) none of these
       c) becomes 1/4th
       d) becomes half

    4. OR

       When spring is compressed, its potential energy:

       a) none of these
       b) decrease
       c) first increase then decrease
       d) increase
    5. What type of energy is stored in the spring of a watch?
       a) potential energy
       b) none of these
       c) mechanical energy
       d) kinetic energy
34. Read the text carefully and answer the questions:
    In a gas the particles are always in a state of random motion, all the particles move at different speed constantly colliding and changing their speed and direction, as speed increases it will result in an increase in its kinetic energy.
    
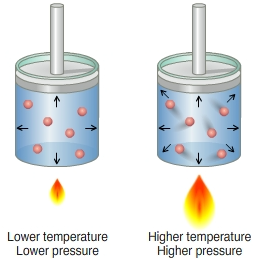
    1. If the temperature of the gas increases from 300 K to 600 K then the average kinetic energy becomes:
       a) same
       b) becomes double
       c) becomes half
       d) none of these
    2. What is the average velocity of the molecules of an ideal gas?
       a) Infinite
       b) Same
       c) None of these
       d) Zero
    3. Cooking gas containers are kept in a lorry moving with uniform speed. The temperature of the gas molecules inside will ________.
       a) decrease
       b) none of these
       c) increase
       d) remains same
    4. Find the ratio of average kinetic energy per molecule of Oxygen and Hydrogen:
       a) 1:1
       b) 4:1
       c) 1:2
       d) 1:4

    5. OR

       The velocities of the three molecules are 3v, 4v, and 5v. calculate their root mean square velocity?

       a) 4.0 v
       b) 4.02 v
       c) 4.08 v
       d) 4.04 v

    To practice more questions & prepare well for exams, download myCBSEguide App. It provides complete study material for CBSE, NCERT, JEE (main), NEET-UG and NDA exams. Teachers can use Examin8 App to create similar papers with their own name and logo.

35. Section E
36. A person normally weighing 50 kg stands on a mass less platform which oscillates up and down harmonically at a frequency of 2.0 s^–1 and an amplitude 5.0 cm. A weighing machine on the platform gives the persons weight against time.
    1. Will there be any change in weight of the body, during the oscillation? Figure In extensible string.
    2. If answer to part (a) is yes, what will be the maximum and minimum reading in the machine and at which position?

    OR

    The motion of a particle executing simple harmonic motion is described by the displacement function, x(t) = Acos({tex}\omega{/tex}t + {tex}\phi{/tex}) If the initial (t = 0) position of the particle is 1 cm and its initial velocity is {tex}\omega{/tex} cm /s, then what are its amplitude and initial phase angle? The angular frequency of the particle is {tex}\pi{/tex} s^-1. If instead of the cosine function, we choose the sine function to describe the SHM, x = Bsin({tex}\omega{/tex}t + {tex}\phi{/tex}), then what are the amplitude and initial phase of the particle with the above initial conditions?

37. A marble rolls along a table at a constant speed of 1.00 m/s and then falls off the edge of the table to the floor 1.00 m below,
    1. How long does the marble take to reach the floor?
    2. At what horizontal distance from the edge of the table does the marble land?
    3. What is its velocity as it strikes the floor?

    OR

    1. What is the angle between {tex}\overrightarrow A{/tex} and {tex}\overrightarrow B{/tex} if {tex}\overrightarrow A{/tex} and {tex}\overrightarrow B{/tex} denote the adjacent sides of a parallelogram drawn form a point and the area of the parallelogram is{tex}\frac { 1 } { 2 } A B{/tex}?
    2. State and prove triangular law of vector addition.
38. A particle of mass m is released from point P at x = x₀ on the X-axis from origin O and falls vertically along the Y-axis, as shown in Fig.
    
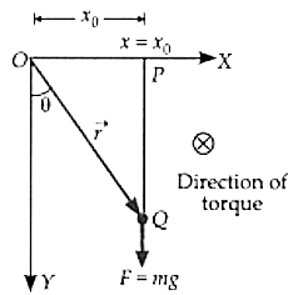
    1. Find the torque t acting on the particle at a time t when it is at point Q with respect to O.
    2. Find the angular momentum L of the particle about O at this time t.
    3. Show that {tex}\tau=\frac{d L}{d t}{/tex} in this example.

    OR

    A uniform disc of radius R, is resting on a table on its rim. The coefficient of friction between disc and table is {tex}\mu{/tex} (Figure).
    
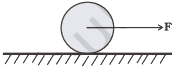
    Now the disc is pulled with a force {tex}\vec { F }{/tex} as shown in the figure. What is the maximum value of F for which the disc rolls without slipping?

Class 11 – Physics Sample Paper Solution (2023-24)

You are getting not only the question paper but also a complete solution with a step-by-step explanation. The solution of the question paper is based on the latest guidelines issued by CBSE for the session 2023-24.

To get more model papers with solutions, you can download the myCBSEguide app or visit https://mycbseguide.com/dashboard/. CBSE has reduced the course content for class 11 Physics. This question paper and solution is based on the updated and reduced syllabus of CBSE for 2023-24.

Class 11 Physics Sample Paper Solution Section A

1. (c) 1.9 {tex}\times{/tex} 10¹²
   Explanation: According to the problem,
   Young’s modulus, Y = 1.9 {tex}\times{/tex} 10¹¹ N/m²
   1N in SI system of units = 10⁵ dyne in C.G.S system.
   Hence, Y = 1.9 {tex}\times{/tex} 10¹¹ {tex}\times{/tex} 10⁵ dyne/m²
   In C.G.S length is measured in unit cm, so we should also convert m into cm.
   {tex}\therefore{/tex} Y = {tex}1.9 \times 10^{11}\left(\frac{10^{5} \mathrm{dyne}}{10^{4} \mathrm{cm}^{2}}\right){/tex} [{tex}\because{/tex} 1m = 100 cm] = 1.9 {tex}\times{/tex} 10¹² dyne/cm²
2. (d) 20 to 20000 Hz
   Explanation: Humans are most sensitive to (i.e. able to discern at lowest intensity) frequencies between 2,000 and 5,000 Hz. The human ear can respond to minute pressure variations in the air if they are in the audible frequency range, roughly 20 Hz – 20 kHz. This incredible sensitivity is enhanced by an effective amplification of the sound signal by the outer and middle ear structures.
3. (c) as that point where the total gravitational torque on the body is zero
   Explanation: The point at which the entire weight of a body may be thought of as centered so that if supported at this point the body would balance perfectly, so it can also be defined as that point where the total gravitational torque on the body is zero.
4. (b) Six times that on the earth’s surface
   Explanation: The height to which the liquid rises in a capillary tube is inversion all proportional to the acceleration due to gravity.
   {tex}h=\frac{2 S \cos \theta}{r \rho g}{/tex}
   thus if all other parameters are fixed
   {tex}h \propto\frac{1}{g}{/tex}
   On the surface of the moon, acceleration due to gravity is {tex}1\over6{/tex}th as that on the surface of the earth. Therefore the water will rise to a height 6 times that on earth’s surface.
5. (b) {tex}{\rm{v}} = – \frac{G{m_1}{m_2}}{r}{/tex}
   Explanation: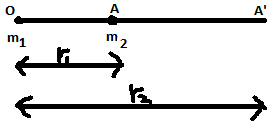
   Change in gravitational potential energy of a system is defined as the -ve of the work done by the gravitational force as the configuration of the system is changed.
   {tex}{U_f}\; – {\rm{ }}{U_i}\; = {\rm{ }}{W_{gr}}=V(Potential Energy){/tex}
   Change in gravitational potential energy of two point masses m₁ and m₂ as their separation is changed from r₁ to r₂ is given by
   {tex}U\left(r_2\right)-U\left(r_1\right)=G m_1 m_2\left[\frac{1}{r_1}-\frac{1}{r_2}\right]{/tex}
   If, at infinite separation, gravitational potential energy is assumed to be zero, then the gravitational potential energy of the above two point mass system at separation r,
   {tex}U(r) =  – G\frac{{m_1}{m_2}} {r}{/tex}
   {tex}\therefore V =  – G\frac{{m_1}{m_2}} { r}{/tex}
   To practice more questions & prepare well for exams, download myCBSEguide App. It provides complete study material for CBSE, NCERT, JEE (main), NEET-UG and NDA exams. Teachers can use Examin8 App to create similar papers with their own name and logo.
6. (b) 105 second ^-1
   Explanation: Frequency of the source = 100 {tex}\pm{/tex} 5 = 105 or 95 Hz
   The second harmonic of the source = 210 Hz or 190 Hz
   As the second harmonic gives 5 beats/sec with a sound of frequency 205 Hz, the second harmonic should be 210 Hz.
   {tex}\therefore{/tex} Frequency of the source = 105 Hz
7. (d) rectilinear motion
   Explanation: Rectilinear motion is another name for straight-line motion. This type of motion describes the movement of a particle or a body. A body is said to experience rectilinear motion if any two particles of the body travel the same distance along two parallel straight lines.
8. (c) 2 {tex}\pi{/tex}A
   Explanation: Maximum particle velocity = Wave velocity
   {tex}\omega A=\frac{\omega}{k}{/tex}
   or {tex}k=\frac{2 \pi}{\lambda}=\frac{1}{A}{/tex}
   {tex}\therefore \lambda{/tex} = 2 {tex}\pi{/tex}A
9. (c) 27 : 1
   Explanation: Excess pressures in the two bubbles will be (1.01 -1) or 0.01 atm and (1.03 – 1) or 0.03 atm.
   {tex}\frac{p_{1}}{p_{2}}=\frac{r_{2}}{r_{1}}{/tex}
   {tex}\Rightarrow \frac{r_{1}}{r_{2}}=\frac{p_{2}}{p_{1}}=\frac{0.03}{0.01}{/tex} = 3
   {tex}\therefore \frac{V_{1}}{V_{2}}=\left(\frac{r_{1}}{r_{2}}\right)^{3}{/tex} = 3³ = 27 : 1
10. (d) Option iv
    Explanation: The required escape velocity of gas molecules is less than their root mean square velocity.
11. (a) 2
    Explanation: As radius of second ring is n times, length and hence mass of wire used is also n times.
    {tex}\therefore \frac{I_{1}}{I_{2}}=\frac{M R^{2}}{n M(n R)^{2}}=\frac{1}{n^{3}}=\frac{1}{8}{/tex} {tex}\therefore n=2{/tex}
12. (b) first decreases and then increases
    Explanation: Density of water is maximum at 4^oC. So during heating from 0^oC to 10^oC, its density increases at first and then it decreases resulting in the decrease in volume at first and then increase in its volume.
13. (a) Assertion and reason both are correct statements and reason is correct explanation for assertion.
    Explanation: In elastic collision, kinetic energy remains conserved therefore the ball rebounds with the same velocity. According to Newton’s second law.
    F {tex}\times{/tex} t = change in linear momentum.
    {tex}\therefore{/tex} F {tex}\times{/tex} 1 = m {tex}\times{/tex}n(u + u) or F = 2mnu
14. (c) Assertion is correct statement but reason is wrong statement.
    Explanation: Assertion is correct statement but reason is wrong statement.
15. (a) Both A and R are true and R is the correct explanation of A.
    Explanation: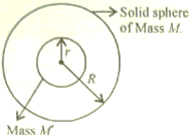
    A uniform shell of matter exerts no gravitational force on a particle located inside it. This also means if a particle is located inside a uniform solid sphere of matter at a distance r from its centre, the gravitational force exerted on the particle is due only to the mass M’ that lies within a sphere of radius r. This mass M’ is given by M’ = {tex}\rho \frac{4 \pi r^{3}}{3}{/tex}, where {tex}\rho{/tex} is the density of the sphere.
16. (d) A is false but R is true.
    Explanation: At the highest point, the instantaneous velocity is acting horizontally and acceleration of projectile (acceleration due to gravity) is acting vertically downward. Therefore, angle between velocity and acceleration at the highest point is 90°.

17. Class 11 Physics Sample Paper Solution Section B

18. We know that, speed of sound, v {tex} \propto \sqrt{T} {/tex}, T being absolute temperature.​​​
    where, T is in kelvin.
    {tex}\therefore \frac{V_{t}}{V_{0}}=\sqrt{\frac{273+t}{273+0}} {/tex} = 3 (say, the required temperature is t℃)
    {tex} \Rightarrow \frac{273+t}{273} {/tex} = 9
    {tex}\Rightarrow{/tex} t = (9 {tex}\times{/tex} 273) – 273 = 2184°C
19. Since, {tex}e ^ { – ( a z / \theta ) }{/tex} is dimensionless (exponential function), we have {tex}a z / \theta = 1{/tex}
    or, {tex}a = \frac { \theta } { Z } = \frac { K } { L } = \left[ \mathrm { L } ^ { – 1 } \mathrm { K } \right]{/tex}
    We find that a/b = dimensions of pressure (because {tex}e ^ { – ( a z / \theta ) }{/tex} is dimensionless)
    a/b = [ML^-1T^-2] Therefore,
    {tex}b = \frac { a } { \left[ \mathrm { ML } ^ { – 1 } \mathrm { T } ^ { – 2 } \right] } = \frac { \left[ \mathrm { L } ^ { – 1 } \mathrm { K } \right] } { \left[ \mathrm { ML } ^ { – 1 } \mathrm { T } ^ { – 2 } \right] }{/tex}
    = [M^-1T²K]
20. Let T = K p^a d^b E^c,
    where K = a dimensionless constant.
    Putting the dimensions of various quantities,
    T = [ML^-1 T^-2]^a [ML^-3]^b [ML² T^-2]^c
    or M⁰L⁰T = M^{a +b + c} L^{~a ~3b + 2c} T^{-2a – 2c}
    Equating the powers of M, L and T on both sides, we get
    a + b + c = 0, – a – 3b + 2c = 0, – 2a – 2c = 1
    On solving,
    a = {tex}-\frac{5}{6}{/tex}, b = {tex}\frac{1}{2}{/tex}, c = {tex}\frac{1}{3}{/tex}
21. Here m₁ = 4 kg, m₂, = 5 kg
    Force applied on block A = 12 N
    This force must atleast be equal to the kinetic friction applied on A by B.
    {tex}\therefore{/tex} 12 = f_k = {tex}\mu_k{/tex} R = {tex}\mu_k{/tex} m₁ g
    or 12 = {tex}\mu_k{/tex} {tex}\times{/tex} 4 g
    or {tex}\mu_{k}=\frac{12}{4 g}=\frac{3}{g}{/tex}
    The block B is on a smooth surface. Hence to move A and B together, the (maximum) force F that can be applied on B is equal to the frictional forces applied on A by B and applied on B by A.
    F = {tex}\mu_k{/tex} m₁g + {tex}\mu_k{/tex} m₂ g = {tex}\mu_k{/tex} (m₁ + m₂)g
    {tex}=\frac{3}{g}{/tex}(4 + 5)g = 27 N
    As this force moves both the blocks together on a smooth table, so the acceleration produced is
    {tex}a=\frac{F}{m_{1}+m_{2}}=\frac{27}{4+5}{/tex} = 3 ms^-2
22. Te = 1 year R_J = 5.2 R_e
    According to the Kepler’s third law
    T² is directly proportional R³
    {tex}\left( \frac { T _ { J } } { \overline { T } e } \right) ^ { 2 } = \left( \frac { R _ { J } } { \mathrm { Re } } \right) ^ {3 }{/tex}
    T_J = (5.2) {tex}\frac 32{/tex} {tex}\times{/tex} 1year
    T_J = 11.86 year

    OR

    The inertial mass of a body is a measure of its inertia and is given by the ratio of the external force applied on it to the acceleration produced in it. The gravitational mass of a body, on the other hand, is a measure of the gravitational pull acting on it due to the earth. The gravitational mass is measured by a common balance.

23. Class 11 Physic Sample Paper Solution Section C

24. Radius of each small drop, r = 1 mm = 0.1 cm
    Terminal velocity of each small drop, v = 5 cms^-1
    Volume of bigger drop = Volume of 8 small drops
    {tex}\frac{4}{3} \pi R^{3}=8 \times \frac{4}{3} \pi r^{3}{/tex}
    or R = 2r = 2 {tex}\times{/tex} 0.1 cm = 0.2 cm
    Terminal velocity of each small drop is given by
    v = {tex}=\frac{2}{9} \frac{r^{2}}{\eta}\left(\rho-\rho^{\prime}\right) \mathrm{g}{/tex} …(i)
    Terminal velocity of bigger drop is given by
    V = {tex}\frac{2}{9} \frac{R^{2}}{\eta}\left(\rho-\rho^{\prime}\right) g{/tex} …(ii)
    Dividing equation (ii) by (i), we get
    {tex}\frac{V}{v}=\frac{R^{2}}{r^{2}}{/tex}
    or V = {tex}v \times \frac{R^{2}}{r^{2}}=5 \times \frac{(0.2)^{2}}{(0.1)^{2}}{/tex}
    = 5 {tex}\times{/tex} 4 = 20 cms^-1
25. Since, co-efficient of linear expansion, {tex}\alpha{/tex} = {tex}\frac { \Delta L } { L \Delta T }{/tex}
    {tex}\Delta L{/tex} = change in length
    L = length
    {tex}\Delta T{/tex} = change in temperature, for an infinitesimally small change in temperature
    {tex}\alpha = \frac{dL}{LdT}{/tex}
    Similarly, co-efficient of superficial expansion, {tex}\beta{/tex} = {tex}\frac {d S } { S dT }{/tex}
    dS = infinitesimal change in area
    S = original area
    dT = infintesimaly change in temperature
    S = L², {tex}\beta= \frac{1}{L^2}\frac{dL^2}{dT} = 2L\frac{dL}{dT}{/tex}
    {tex}\beta = 2\alpha{/tex}
    Similarly, co-efficient of cubical expansion, {tex}\gamma = \frac {dV}{VdT}{/tex}
    dV = infinitesimal change in volume
    V = original volume
    dT = infinitesimal change in temperature
    {tex}\gamma = \frac{1}{L^3}\frac{dL^3}{dT} = 3\frac{1}{L}\frac{dL}{dT} =3\alpha{/tex}
    {tex}\alpha = \frac { \beta } { 2 } = \frac { \gamma } { 3 }{/tex}
26. When the parachutist falls freely :
    u = 0, v = 9.8 ms^-2, s = 40m, t = ?, u = ?
    As s = ut + {tex}\frac{1}{2} g t^{2}{/tex}
    {tex}\therefore 40=0+\frac{1}{2} \times 9.8 \times t^{2}{/tex}
    or t = {tex}\sqrt{\frac{80}{9.8}}=\frac{20}{7} \mathrm{~s}{/tex} = 2.86 s
    Also, v = u + gt = 0 + 9.8 {tex}\times \frac{20}{7}{/tex} = 28 ms^-1
    When the parachutist decelerates uniformly:
    u = 28 ms^-1, a = -2 ms^-2, 5 = 2 ms^-1
    Time taken, t = {tex}\frac{v \ – \ u}{a}=\frac{2 \ – \ 28}{-2}{/tex} = 13 s
    Distance, s = ut + {tex}\frac{1}{2} at^{2}{/tex} = 28 {tex}\times{/tex} 13 {tex}-\frac{1}{2} \times{/tex} 2 {tex}\times{/tex} (13)²
    = 364 – 169 = 195 m
    Total time of parachutist in air
    = 2.86 + 13 = 15.86 s
    Height at which parachutist bails out
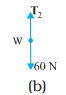
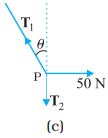
    = 40 + 195 = 235 m
27. Figure (b) and (c) are known as free-body diagrams. Figure (b) is the free-body diagram of W and Figure (c) is the free-body diagram of point P.
    Consider the equilibrium of the weight W. Clearly, T₂ = 6 {tex}\times{/tex} 10 = 60 N. Consider the equilibrium of the point P under the action of three forces – the tensions T₁ and T₂, and the horizontal force 50 N. The horizontal and vertical components of the resultant force must vanish separately:
    T₁ cos{tex}\theta{/tex} = T₂ = 60N
    T₁ sin{tex}\theta{/tex} = 50 N
    Which gives that
    {tex}\tan \theta=\frac{5}{6}{/tex} or {tex}=\tan ^{-1}\left(\frac{5}{6}\right)=40^{\circ}{/tex}
    Note the answer does not depend on the length of the rope (assumed massless) nor on the point at which the horizontal force is applied.
    1. {tex}\because{/tex} process is adiabatic
       {tex}\therefore{/tex} {tex}\Delta{/tex} = 0
       Work done on the gas, {tex}\Delta{/tex}W = -500J
       According to the first law of thermodynamics.
       {tex}\Delta{/tex}Q = {tex}\Delta{/tex}U + {tex}\Delta{/tex}W {tex}\Rightarrow{/tex} {tex}\Delta{/tex}U = –{tex}\Delta{/tex}W = 500J
    2. This is because heat absorbed by a substance (coolant) is directly proportional to the specific heat of the substance.
    3.  This is because in a harbour town, the relative humidity is more than in a desert town. Hence, the climate of a harbour town is without extremes of hot and cold.
28. Conveyor belt is accelerating with 1 m/s². A man is stationary with respect to horizontal conveyor belt
    Hence, acceleration of man = acceleration of belt = 1m/s²
    Hence, Net force on the man = ma = 65 {tex}\times{/tex} 1 = 65 N direction of this force is opposite to direction of conveyor belt.
    Coefficient of friction between the man’s shoes and belt = 0.2. Let a’ is the acceleration of the belt can the man continue to be stationary relative to the belt.
    In equilibrium condition,
    Friction force = ma’
    0.2 {tex}\times{/tex} m {tex}\times{/tex} g = ma’
    a’ = 0.2 {tex}\times{/tex} g = 0.2 {tex}\times{/tex} 10 = 2m/s²
29. PASCAL LAW :-
    One of the most important facts about fluid pressure is that a change in pressure at one part of the liquid will be transmitted without any change to other parts. This rule is known as Pascal’s law.
    Take a vessel containing a liquid in the equilibrium at rest. Consider a volume element of liquid of height h. In the absence of gravity, according to Pascal’s law, the pressure at the upper section A and lower section B of the volume element should be same.
    However, taking gravity into consideration we find the following forces acting on the said volume element:
    1. Force P₁ ({tex}\Delta A{/tex}) acting vertically downward at the top face A,
    2. Force P₂ ({tex}\Delta A{/tex}) acting vertically upward at the bottom face B, and

    Weight mg of the liquid in the volume element acting vertically downwards. Here, {tex}\Delta A{/tex} is the cross-section area of the given volume element.
    For volume element to be in equilibrium net force acting on it should be zero. Therefore, we have
    {tex}P_1\triangle A + mg – P_2\triangle A = 0\ or\ P_1\triangle A + mg = P_2\triangle A{/tex}
    But m = mass of volume element = {tex}\Delta A{/tex}.h.{tex}\rho{/tex}, where {tex}\rho{/tex} = density of the liquid
    {tex}\therefore{/tex} {tex}P_1\triangle A + \triangle A h\rho g = P_2\triangle A{/tex}
    {tex}\Rightarrow{/tex} {tex}P_2 = P_1 + h\rho g{/tex}
    According to the above equation, if the pressure P₁ is increased in any way, the pressure P₂ must increase by exactly the same amount.
    The pressure applied to any part of an enclosed liquid at rest is transmitted undiminished to every portion of the liquid as well as the walls of the container.

    OR

    Let h be the height of the liquid column of density {tex}\rho{/tex} taken in the cylindrical vessel of radius r.
    Force exerted by the liquid on the bottom of the vessel = Total weight of the liquid column
    = mg = {tex}\pi r^{2} h \rho g{/tex}
    Area of the sides of the vessel = 2 {tex}\pi{/tex}rh
    Average pressure exerted by the liquid on the sides of the vessel
    = {tex}\frac{\text { Pressure at the top }+\text { Pressure at the bottom }}{2}{/tex}
    = {tex}=\frac{0+h \rho g}{2}=\frac{1}{2} h \rho g{/tex}
    Force exerted by the liquid on the sided of the vessel
    = Pressure {tex}\times{/tex} Area = {tex}\frac{1}{2} h \rho g \times 2 \pi r h{/tex}
    As the above two forces are given to be equal, so
    {tex}\frac{1}{2} h \rho g \times 2 \pi r h=\pi r^{2} h \rho g{/tex} or h = r
    i.e., Height of liquid column
    = Radius of the cylindrical vessel.

30. Class 11 Physics Sample Paper Section D Solution

31. 1. (c) 2:1
       Explanation: 2:1
    2. (d) heavy body
       Explanation: heavy body
    3. (a) becomes double
       Explanation: becomes double

    4. OR

       (d) increase
       Explanation: increase

    5. (a) potential energy
       Explanation: potential energy
32. 1. (b) becomes double
       Explanation: becomes double
    2. (d) Zero
       Explanation: Zero
    3. (d) remains same
       Explanation: remains same
    4. (a) 1:1
       Explanation: 1:1

    5. OR

       (c) 4.08 v
       Explanation: 4.08 v

33. Class 11 Physics Sample Paper Section E Solution

    1. Weight in weight machine will be due to the normal reaction (N) by platform. Consider the top position of platform, two forces acting on it are due to weight of person and oscillator. They both act downward.
       
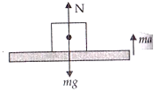
       (mg = weight of the person with the oscillator is acting downwards, ma = force due to oscillation is acting upwards, N = normal reaction force acting upwards)
       {tex}{/tex}Now for the downward motion of the system with an acceleration a,
       ma = mg – N …..(i)
       {tex}{/tex}When platform lifts form its lowest position to upward
       ma = N – mg ……(ii)
       {tex} a = \omega ^ { 2 } A{/tex}  is value of acceleration of oscillator
       {tex}\therefore{/tex} From equation (i) we get,
       {tex} N = m g – m \omega ^ { 2 } A{/tex}
       {tex}{/tex}Where A is amplitude, {tex}\omega{/tex} angular frequency and m mass of oscillator.
       {tex}\omega=2\pi\nu{/tex}
       {tex}\therefore\omega = 2 \pi \times 2 = 4 \pi ~r a d / \mathrm { sec }{/tex}
       Again using {tex}A = 5 ~ c m = 5 \times 10 ^ { – 2 } m {/tex} we get
       {tex}N = 50 \times 9.8 – 50 \times 4 \pi \times 4 \pi \times 5 \times 10 ^ { – 2 }{/tex}
       {tex}= 50 \left[ 9.8 – 16 \pi ^ { 2 } \times 5 \times 10 ^ { – 2 } \right]{/tex}N
       {tex}= 50 \left[ 9.8 – 80 \times 3.14 \times 3.14 \times 10 ^ { – 2 } \right]{/tex}N
       {tex}\Rightarrow N = 50 [ 9.8 – 7.89 ] = 50 \times 1.91 = 95.50 \mathrm { N }{/tex}
       So minimum weight is 95.50 N(for downward motion of the platform)
       From equation (ii), N – mg = ma
       For upward motion from the lowest to the highest point of oscillator,
       {tex} N = m g + m a{/tex}
       {tex}= m \left[ 9.81 + \omega ^ { 2 } A \right] \quad \!\! \because a = \omega ^ { 2 } A{/tex}
       {tex}= 50 \left[ 9.81 + 16 \pi ^ { 2 } \times 5 \times 10 ^ { – 2 } \right]{/tex}
       {tex}= 50 [ 9.81 + 7.89 ] = 50 ×17.70 {/tex}N = 885 N
       Hence, there is a change in weight of the body during oscillation.
    2. The maximum weight is 885 N, when platform moves from lowest to upward direction.
       And the minimum weight is 95.5 N, when platform moves from the highest point to downward direction.
34. As the marble was rolling on the table, therefore it has horizontal velocity and it will act as a projectile as soon as it leaves the edge of the table and fall freely under the effect of gravity.
    Since, the marble is initially moving horizontally, v_y0 = 0 and v_x0 = 1.00 m/s. We must consider the origin to be at the edge of the table, so that x₀ = y₀ = 0
    
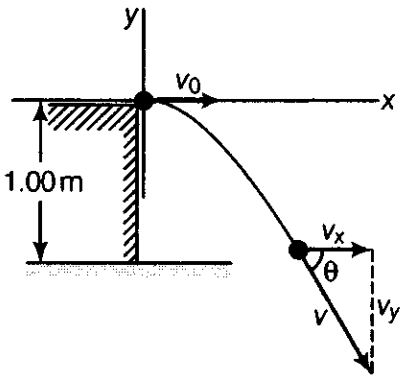
    1. t = ? and y = -1.00 m
       {tex}\therefore{/tex} y = {tex}\frac{-1}{2}{/tex}gt²
       {tex}\Rightarrow t = \sqrt { \frac { – 2 y } { g } } = \sqrt { \frac { ( – 2 ) ( – 1.00 ) } { 9.8 } }{/tex}= 0.452 s
    2. x = ?, when t = 0.452 s
       {tex}\therefore{/tex} x = v_x0t = 1.00 {tex}\times{/tex} 0.452 s = 0.452 m
    3. v = ?, {tex}\theta {/tex} = ? at t = 0.452 s
       The x-component of velocity is constant throughout the motion,
       v_x = v_x0 = 1.00 m/s
       The y-component of velocity is given by
       v_y = v_y0 – gt = 0 – 9.8 {tex}\times{/tex} 0.452 = – 4.43 m/s
       {tex}\therefore v = \sqrt { v _ { x } ^ { 2 } + v _ { y } ^ { 2 } }{/tex} {tex}= \sqrt { ( 1.00 ) ^ { 2 } + ( – 4.43 ) ^ { 2 } }{/tex} = 4.54 m/s, the magnitude of the resultant velocity of the motion.
       {tex}\theta = \tan ^ { – 1 } \left| \frac { v _ { y } } { v _ { x } } \right| = \frac { 4.43 } { 1.00 } = 77.3 ^ { \circ }{/tex}
       As the marble hits the floor, its velocity is 4.54 m/s directed 77.3° downward with respect to the horizontal.

    OR

    1. Area of a parallelogram {tex}= | \vec { A } \times \vec { B } |{/tex} = {tex}A B \sin \theta{/tex} ({tex}\therefore{/tex} Applying cross product)
       Given, area of parallelogram {tex}= \frac { 1 } { 2 } A B{/tex}
       So, {tex}\frac { 1 } { 2 } A B = A B \sin \theta{/tex}
       {tex}\frac { 1 } { 2 } = \sin \theta{/tex}
       {tex}\theta = \sin ^ { – 1 } \left( \frac { 1 } { 2 } \right){/tex}
       {tex}\theta = 30 ^ { \circ }{/tex}
    2. Triangular law of vector addition states that if two vectors can be represented both in magnitude and direction by the sides of a triangle taken in order then their resultant is given by the third side of the triangle taken in opposite order.
       Proof: in {tex}\triangle{/tex}ADC
       {tex}( O C ) ^ { 2 } = ( O D ) ^ { 2 } + ( D C ) ^ { 2 }{/tex}
       
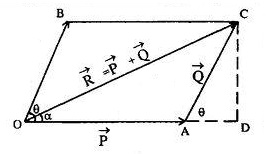
       {tex}( O C ) ^ { 2 } = ( O A + A D ) ^ { 2 } + ( D C ) ^ { 2 }{/tex}
       {tex}(OC)^2\;=\;(OA)^2\;+\;(AD)^2\;+\;2(OA)(AD)\;+\;(DC)^2{/tex}
       {tex}( OC ) ^ { 2 } = \left( P ^ { 2 } \right) + ( Q \cos \theta ) 2 + 2 ( P ) ( Q \cos \theta ) + ( Q \sin \theta ) ^ { 2 }{/tex}
       {tex}\begin{array}{l}(OC)^2=P^2+Q^2\left(\sin^2\theta+\cos^2\theta\right)+2PQ\cos\theta\;\;\;\left(\because\frac{CD}{AC}=\sin\left(\theta\right)\;,\;\;\frac{AD}{AC}=\cos\left(\theta\right)\right)\\\end{array}{/tex}
       {tex}( R ) ^ { 2 } = P ^ { 2 } + Q + 2 P Q \cos \theta \left( \because \sin ^ { 2 } \theta + \cos ^ { 2 } Q \right){/tex}
       {tex}R=\sqrt{P^2+Q^2+2PQ\cos\theta}{/tex}

    To practice more questions & prepare well for exams, download myCBSEguide App. It provides complete study material for CBSE, NCERT, JEE (main), NEET-UG and NDA exams. Teachers can use Examin8 App to create similar papers with their own name and logo.

    1. The force of gravity, F= mg produces the torque {tex}\tau{/tex}. Let {tex}\vec{r}{/tex} be the position vector of Q. Then the magnitude of the torque is given by
       {tex}\tau=r F \sin \theta{/tex}
       {tex}=r \times m g \times \frac{x_{0}}{r}=m g x_{0}{/tex} {tex}\left[\because \sin \theta=\frac{x_{0}}{r}\right]{/tex}
       The direction of the torque is directed into the plane of paper and perpendicular to it, as shown by {tex}\otimes{/tex}.
    2. The magnitude of the angular momentum is {tex}L=r p \sin \theta=r m v \sin \theta{/tex}
       But the velocity v at point Q is given by v = u + at = 0 + gt = gt
       {tex}\therefore \quad L=r m g t . \frac{x_{0}}{r}=m g x_{0} t{/tex}
       The direction of angular momentum is the same as that of torque.
    3. Now L = mgx₀t
       Differentiating both sides with respect to f, we get
       {tex}\frac{d L}{d t}=\frac{d}{d t}\left(m g x_{0} t\right)=m g x_{0}=\tau{/tex}
       Hence the relation {tex}\tau=\frac{d L}{d t}{/tex} holds in this example.

CBSE Sample Papers for Class 11

• Physics
• Chemistry
• Mathematics
• Biology
• Accountancy
• Economics
• Business Studies
• Computer Science
• Informatics Practices
• English Core
• Hindi Core
• Hindi Elective
• History
• Political Science
• Geography
• Sociology
• Physical Education
• Other Subjects

To download sample papers for class 11 Physics, Chemistry, Biology, History, Political Science, Economics, Geography, Computer Science, Home Science, Accountancy, Business Studies and Home Science; do check myCBSEguide app or website. myCBSEguide provides sample papers with solutions, test papers for chapter-wise practice, NCERT solutions, NCERT Exemplar solutions, quick revision notes for ready reference, CBSE guess papers and CBSE important question papers. Sample Papers all are made available through the best app for CBSE students and myCBSEguide website.

Test Generator

Create question paper PDF and online tests with your own name & logo in minutes.

Create Now

myCBSEguide

Question Bank, Mock Tests, Exam Papers, NCERT Solutions, Sample Papers, Notes

Install Now